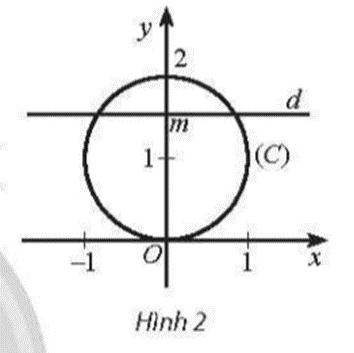
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x^2 + (y ‒ 1)^2 = 1. Với mỗi số thực m gọi Q(m)

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x + (y ‒ 1) = 1. Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng d: y = m với đường tròn (C). Viết công thức xác định hàm số y = Q(m). Hàm số này không liên tục tại các điểm nào?

Giải sách bài tập Toán 11 Bài 3: Hàm số liên tục - Chân trời sáng tạo

Bài 11 trang 91 SBT Toán 11 Tập 1: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x² + (y ‒ 1)² = 1. Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng d: y = m với đường tròn (C). Viết công thức xác định hàm số y = Q(m). Hàm số này không liên tục tại các điểm nào?

Lời giải:

$\mathrm{Ta} \mathrm{có}: \mathrm{Q}\mathrm{(m)} = \left\{\begin{array}{l}0 \mathrm{khi} \mathrm{m} < 0 \mathrm{hay} \mathrm{m} > 2\\ 1 \mathrm{khi} \mathrm{m} = 0 \mathrm{hay} \mathrm{m} = 2\\ 2 \mathrm{khi} 0 < \mathrm{m} < 2\end{array}\right.$

Ta có $\underset{m\to 0^{-}}{\lim }Q\left(m\right)=0;\underset{m\to 0^{+}}{\lim }Q\left(m\right)=2;f\left(0\right)=1$

nên $\underset{m\to 0^{-}}{\lim }Q\left(m\right)\ne \underset{m\to 0^{+}}{\lim }Q\left(m\right)\ne f\left(0\right)$

Do đó hàm số y = Q(m) không liên tục tại m = 0.

Tương tự ta cũng có hàm số y = Q(m) không liên tục tại m = 2.

Vậy hàm số không liên tục tại các điểm m = 0 và m = 2.

Lời giải Sách bài tập Toán lớp 11 Bài 3: Hàm số liên tục hay khác:

• Bài 1 trang 90 SBT Toán 11 Tập 1: Dùng định nghĩa, xét tính liên tục của hàm số: ....

• Bài 2 trang 90 SBT Toán 11 Tập 1: Xét tính liên tục của mỗi hàm số sau tại điểm x = 2. ....

• Bài 3 trang 90 SBT Toán 11 Tập 1: Xét tính liên tục của hàm số: ....

• Bài 4 trang 90 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\left\{\begin{array}{cc}\frac{\sqrt{x+2}-2}{x-2}& \text{ khi }x\ne 2\\ a& \text{ khi }x=2.\end{array}\right.$ ....

• Bài 5 trang 90 SBT Toán 11 Tập 1: Xét tính liên tục của các hàm số sau: ....

• Bài 6 trang 90 SBT Toán 11 Tập 1: Xét tính liên tục của các hàm số sau: ....

• Bài 7 trang 90 SBT Toán 11 Tập 1: Cho hai hàm số f(x) = x ‒ 1 và g(x) = x² ‒ 3x + 2. Xét tính liên tục của các hàm số: ....

• Bài 8 trang 91 SBT Toán 11 Tập 1: Cho hai hàm số $f\left(x\right)=\left\{\begin{array}{l}2-x\text{ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}khi }x<1\\ x^2+x\text{ khi }x\ge 1\end{array}\right.$ và $g\left(x\right)=\left\{\begin{array}{l}2x-x^2\text{ khi }x<1\\ -x^2+a\text{ khi }x\ge 1.\end{array}\right.$....

• Bài 9 trang 91 SBT Toán 11 Tập 1: Cho hàm số $y=f\left(x\right)=\left\{\begin{array}{l}{x}^2+ax+b\text{ khi }\left|x\right|<2\\ x\left(2-x\right)\text{\hspace{0.17em} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}khi }\left|x\right|\ge 2\end{array}\right..$ Tìm giá trị của các tham số a và b sao cho hàm số y = f(x) liên tục trên ℝ. ....

• Bài 10 trang 91 SBT Toán 11 Tập 1: Chứng minh rằng phương trình: a) x³ + 2x ‒ 1 = 0 có nghiệm thuộc khoảng (‒1; 1). ....

• Bài 12 trang 91 SBT Toán 11 Tập 1: Cho nửa đường tròn đường kính AB = 2. Đường thẳng d thay đổi luôn đi qua A ....