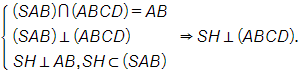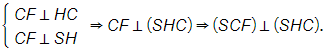Cho hình chóp S ABCD có đáy ABCD là hình chữ nhật AB = 2a BC = a mặt bên SAB
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC = a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E là trung điểm của CD. Tính theo a khoảng cách giữa hai đường thẳng BE và SC.
Giải sách bài tập Toán 11 Bài tập cuối chương 8 - Chân trời sáng tạo
Câu 10 trang 75 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC = a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E là trung điểm của CD. Tính theo a khoảng cách giữa hai đường thẳng BE và SC.
A. .
B. .
C. .
D. a.
Lời giải:
Đáp án đúng là: A
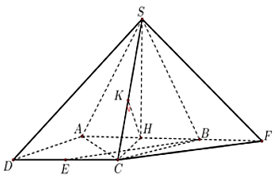
Gọi H là trung điểm AB.
Do 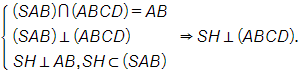
F đối xứng với H qua B BECF là hình bình hành.
BE // CF (SCF) d(BE, (SCF)) = d(B, (SCF)) = d(H, (SCF)).
HBCE là hình vuông cạnh a
Dễ thấy ∆HCF vuông cân tại C.
Khi này 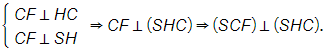
Mà (SCF) (SHC) = SC. Trong (SHC) kẻ HK ⊥ SC HK ⊥ (SCF).
Suy ra d(H, (SCF)) = HK d(BE, SC) = HK.
Áp dụng hệ thức lượng trong ∆SHC vuông tại H, đường cao HK
.
Vậy .
Lời giải SBT Toán 11 Bài tập cuối chương 8 hay khác:
Câu 14 trang 75 SBT Toán 11 Tập 2: Gọi V là thể tích của hình lập phương ABCD.A'B'C'D'. V1 là thể tích của tử diện A'ABD Hệ thức nào sau đây là đúng? ....
Bài 1 trang 76 SBT Toán 11 Tập 2: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). ....
Bài 2 trang 76 SBT Toán 11 Tập 2: Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Vẽ các đường cao BE, DF của tam giác BCD ....
Bài 3 trang 76 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB ....
Bài 4 trang 76 SBT Toán 11 Tập 2: Cho khối chóp tam giác S.ABC có SA ⊥ (ABC), tam giác ABC có độ dài 3 cạnh là AB = 5a, BC = 8a, AC = 7a, góc giữa SB và (ABC) ....
Bài 5 trang 76 SBT Toán 11 Tập 2: Cho hình lăng trụ đứng có đáy ABC là tam giác vuông tại B. Biết AB = a, BC = , góc giữa hai mặt phẳng () và (ABC) bằng 60°. ....
Bài 6 trang 76 SBT Toán 11 Tập 2: Cho khối lăng trụ đứng có đáy ABC là tam giác cân với AB = AC = a, , mặt phẳng (AB'C') tạo với đáy một góc 60°. ....
Bài 7 trang 76 SBT Toán 11 Tập 2: Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B'AC) tạo với đáy một góc 30°, khoảng cách từ B ....
Bài 8 trang 76 SBT Toán 11 Tập 2: Một thùng đựng rác có dạng hình chóp cụt tứ giác đều. Đáy và miệng thùng có độ dài lần lượt là 60 cm và 120 cm, cạnh bên ....