Trong một ngày, tổng chi phí để một xưởng sản xuất x (kg) thành phẩm
Trong một ngày, tổng chi phí để một xưởng sản xuất x (kg) thành phẩm được cho bởi hàm số C(x) = 2x – 30x + 177x + 2 592 (nghìn đồng). Biết giá bán mỗi kilôgam thành phẩm là 513 nghìn đồng và công suất tối đa của xưởng 20 kg trong một ngày. Khối lượng thành phẩm xưởng nên sản xuất trong trong một ngày là bao nhiêu để lợi nhuận thu được của xưởng trong một ngày là cao nhất?
Giải SBT Toán 12 Chân trời sáng tạo Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Bài 11 trang 18 SBT Toán 12 Tập 1: Trong một ngày, tổng chi phí để một xưởng sản xuất x (kg) thành phẩm được cho bởi hàm số C(x) = 2x3 – 30x2 + 177x + 2 592 (nghìn đồng). Biết giá bán mỗi kilôgam thành phẩm là 513 nghìn đồng và công suất tối đa của xưởng 20 kg trong một ngày. Khối lượng thành phẩm xưởng nên sản xuất trong trong một ngày là bao nhiêu để lợi nhuận thu được của xưởng trong một ngày là cao nhất?
Lời giải:
Lợi nhuận xưởng thu được trong một ngày khi sản xuất x (kg) thành phẩm là:
P(x) = 513x – (2x3 – 30x2 + 177x + 2 592) = −2x3 + 30x2 + 336x – 2 592 với 0 ≤ x ≤ 20.
Ta có: P'(x) = −6x2 + 60x + 336
P'(x) = 0 ⇔ x = 14 hoặc x = −4 (loại do −4 ∉ [0; 20]).
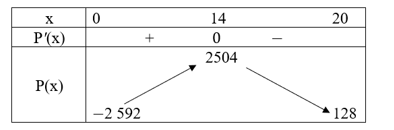
Ta có bảng biến thiên:
Do đó .
Vậy x = 14 kg.
Lời giải SBT Toán 12 Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số hay khác:
Bài 5 trang 17 SBT Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: a) ....