Cho tam giác ABC cân tại A nội tiếp trong đường tròn tâm O, bán kính 1 cm

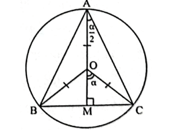
Cho tam giác ABC cân tại A nội tiếp trong đường tròn tâm O, bán kính 1 cm. Đặt = α (0 < α < π).

Giải SBT Toán 12 Chân trời sáng tạo Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Bài 9 trang 18 SBT Toán 12 Tập 1: Cho tam giác ABC cân tại A nội tiếp trong đường tròn tâm O, bán kính 1 cm. Đặt $\hat{A}$ = α (0 < α < π).

a) Viết biểu thức tính diện tích S của tam giác ABC theo α.

b) Tìm diện tích lớn nhất của tam giác ABC.

Lời giải:

Cho tam giác ABC cân tại A nội tiếp trong đường tròn tâm O, bán kính 1 cm

a) Gọi M là trung điểm của BC, ta có $\hat{M O C} = 2 \hat{O A C} = \hat{B A C}$ = α.

Do đó: AM = AO + OM = 1 + cosα,

BC = 2MC = 2sinα.

Suy ra S = $\frac{1}{2}$ AM.BC = sinα(1 + cosα).

b) Ta có: S' = cosα(1 + cosα) – sin²α = 2cos²α + cosα – 1;

S' = 0 ⇔ cosα = −1 hoặc cosα = $\frac{1}{2}$

⇔ α = π + k2π hoặc α = $\pm \frac{π}{3} + k 2 π$ .

Mà 0 < α < π do đó α = $\frac{π}{3}$ .

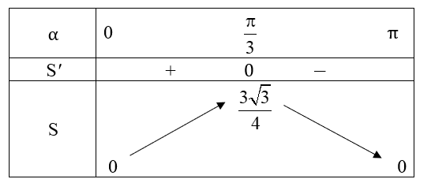
Ta có bảng biến thiên:

Cho tam giác ABC cân tại A nội tiếp trong đường tròn tâm O, bán kính 1 cm

Vậy $\underset{(0; π)}{\max S} = S (\frac{π}{3}) = \frac{3 \sqrt{3}}{4}$ (cm²).

Lời giải SBT Toán 12 Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số hay khác: