Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: y = căn bậc hai (-x^2 + 9)

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

Giải SBT Toán 12 Chân trời sáng tạo Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Bài 5 trang 17 SBT Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) $y = \sqrt{- x^{2} + 9}$ ;

b) y = $\frac{x + 1}{x^{2} + 2 x + 10}$

Lời giải:

a) $y = \sqrt{- x^{2} + 9}$

Tập xác định: D = [−3; 3].

Ta có: y' = $\frac{- x}{\sqrt{- x^{2} + 9}}$

y' = 0 ⇔ $\frac{- x}{\sqrt{- x^{2} + 9}}$ = 0 ⇔ x = 0.

Tính các giá trị, ta được: y(−3) = 0, y(0) = 3, y(3) = 0.

Do đó, $\min_{[- 3; 3]} y = y (3) = y (- 3) = 0$ , $\max_{[- 3; 3]} y = y (0) = 3$ .

b) y = $\frac{x + 1}{x^{2} + 2 x + 10}$

Tập xác định: D = ℝ.

Ta có: y' = $\frac{x^{2} + 2 x + 10 - (x + 1) (2 x + 2)}{{(x^{2} + 2 x + 10)}^{2}}$ = $\frac{- x^{2} - 2 x + 8}{{(x^{2} + 2 x + 10)}^{2}}$

y' = 0 ⇔ x = 2 hoặc x = −4.

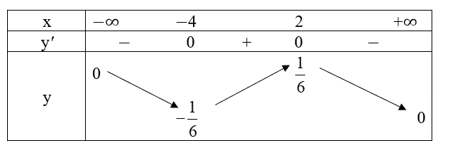
Ta có bảng biến thiên:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: y = căn bậc hai (-x^2 + 9)

Lời giải SBT Toán 12 Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số hay khác: