Từ một miếng bìa hình vuông có cạnh bằng 12 cm, người ta cắt bỏ đi bốn hình vuông
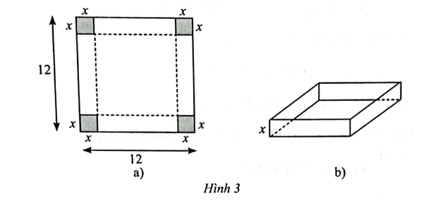
Từ một miếng bìa hình vuông có cạnh bằng 12 cm, người ta cắt bỏ đi bốn hình vuông nhỏ có cạnh bằng x (cm) ở bốn góc (Hình 3a) và gấp lại thành một hình hộp không nắp (Hình 3b). Tìm x để thể tích của hình hộp là lớn nhất.
Giải SBT Toán 12 Chân trời sáng tạo Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Bài 8 trang 18 SBT Toán 12 Tập 1: Từ một miếng bìa hình vuông có cạnh bằng 12 cm, người ta cắt bỏ đi bốn hình vuông nhỏ có cạnh bằng x (cm) ở bốn góc (Hình 3a) và gấp lại thành một hình hộp không nắp (Hình 3b). Tìm x để thể tích của hình hộp là lớn nhất.
Lời giải:
Chiếc hộp sau khi gấp có cạnh đáy là: 12 – 2x (cm) với 0 < x < 6.
Thể tích của chiếc hộp lúc này là: V = x(12 – 2x)2 với 0 < x < 6.
Ta có: V' = (12 – 2x)2 – 4x(12 – 2x) = 12x2 – 96x +144
V' = 0 ⇔ x = 2 hoặc x = 6 (loại do 6 ∉ (0; 6)).
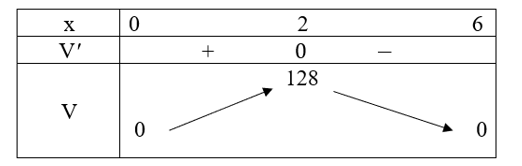
Ta có bảng biến thiên:
Vậy thể tích chiếc hộp lớn nhất là 128 cm3 khi x = 2 (cm).
Lời giải SBT Toán 12 Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số hay khác:
Bài 5 trang 17 SBT Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: a) ....