Một cửa hàng ước tính số lượng sản phẩm q (0 ≤ q ≤ 100) bán được phụ thuộc vào
Một cửa hàng ước tính số lượng sản phẩm q (0 ≤ q ≤ 100) bán được phụ thuộc vào giá bán p (tính bằng nghìn đồng) theo công thức p + 2q = 300. Chi phi cửa hàng cần chi để nhập về q sản phẩm là C(p) = 0,05p – 5,7q + 295q + 300 (nghìn đồng).
Giải SBT Toán 12 Chân trời sáng tạo Bài 1: Tính đơn diệu và cực trị của hàm số
Bài 14 trang 12 SBT Toán 12 Tập 1: Một cửa hàng ước tính số lượng sản phẩm q (0 ≤ q ≤ 100) bán được phụ thuộc vào giá bán p (tính bằng nghìn đồng) theo công thức p + 2q = 300. Chi phi cửa hàng cần chi để nhập về q sản phẩm là C(p) = 0,05p3 – 5,7q2 + 295q + 300 (nghìn đồng).
a) Viết công thức tính lợi nhuận l của cửa hàng khi nhập về và bán được q sản phẩm.
b) Trong khoảng nào của q thì lợi nhuận sẽ tăng khi q tăng, trong khoảng nào thì lợi nhuận giảm khi q tăng?
Lời giải:
a) l = pq – C = q(300 – 2q) – (0,05q3 – 5,7q2 + 295q + 300)
= −0,05q3 + 3,7q2 + 5q – 300.
b) Ta có: l = −0,05q3 + 3,7q2 + 5q – 300
l' = −0,15q2 + 7,4q + 5
l' = 0 ⇔ q = (loại) hoặc q = 50.
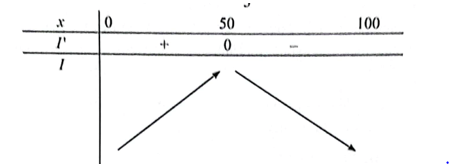
Ta có bảng biến thiên:
Từ đó, lợi nhuận tăng khi q tăng trong khoảng (0; 50), giảm khi q trong khoảng (50; 100).
Lời giải SBT Toán 12 Bài 1: Tính đơn diệu và cực trị của hàm số hay khác:
Bài 3 trang 10 SBT Toán 12 Tập 1: Xét tính đơn điệu và tìm cực trị của các hàm số: a) ....
Bài 4 trang 10 SBT Toán 12 Tập 1: Xét tính đơn điệu và tìm cực trị của các hàm số:a)....
Bài 5 trang 10 SBT Toán 12 Tập 1: Tìm m để a) Hàm số đồng biến trên từng khoảng xác định.....
Bài 7 trang 11 SBT Toán 12 Tập 1: Chứng minh rằng: a) tanx ≥ x với mọi x ∈ ....