Chứng minh rằng: Phương trình x^3 + 5x^2 – 8x + 4 = 0 có duy nhất một nghiệm

Chứng minh rằng:

Giải SBT Toán 12 Chân trời sáng tạo Bài 1: Tính đơn diệu và cực trị của hàm số

Bài 8 trang 11 SBT Toán 12 Tập 1: Chứng minh rằng:

a) Phương trình x³ + 5x² – 8x + 4 = 0 có duy nhất một nghiệm.

b) Phương trình −x³ + 3x² + 24x – 1 = 0 có ba nghiệm phân biệt.

Lời giải:

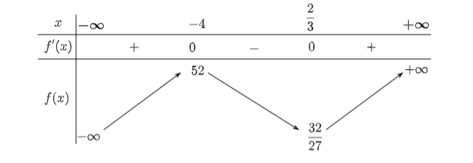
a) Đặt f(x) = x³ + 5x² – 8x + 4

Khi đó, f'(x) = 3x² + 10x – 8.

f'(x) = 0 ⇔ x = $\frac{2}{3}$ hoặc x = −4.

Ta có bảng biến thiên như sau:

Chứng minh rằng: Phương trình x^3 + 5x^2 – 8x + 4 = 0 có duy nhất một nghiệm

Từ bảng biến thiên, ta thấy đường thẳng y = 0 giao với đồ thị của hàm số tại đúng một thời điểm trong khoảng (−∞; −4).

Do đó, phương trình x³ + 5x² – 8x + 4 = 0 có duy nhất một nghiệm.

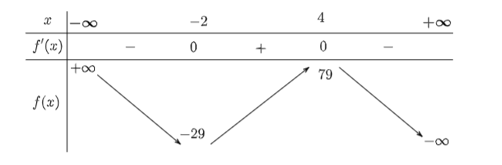
b) Đặt f(x) = −x³ + 3x² + 24x + 1

Ta có: f'(x) = −3x² + 6x + 24

f'(x) = 0 ⇔ x = −2 hoặc x = 4.

Ta có bảng biến thiên như sau:

Chứng minh rằng: Phương trình x^3 + 5x^2 – 8x + 4 = 0 có duy nhất một nghiệm

Từ bảng biến thiên, ta thấy đường thẳng y = 0 giao với đồ thị của hàm số tại ba điểm phân biệt.

Do đó, phương trình −x³ + 3x² + 24x – 1 = 0 có ba nghiệm phân biệt.

Lời giải SBT Toán 12 Bài 1: Tính đơn diệu và cực trị của hàm số hay khác: