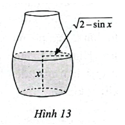
Một bình chứa nước dạng như Hình 13 có chiều cao là 3π/2 dm. Nếu lượng nước trong bình có chiều cao là x (dm)

Một bình chứa nước dạng như Hình 13 có chiều cao là dm. Nếu lượng nước trong bình có chiều cao là x (dm) thì mặt nước là hình tròn có bán kính (dm) với 0 ≤ x ≤ . Tính dung tích của hình (kết quả làm tròn đến hàng phần trăm của đềximét khối).

Giải SBT Toán 12 Chân trời sáng tạo Bài 3: Ứng dụng hình học của tích phân

Bài 6 trang 21 SBT Toán 12 Tập 2: Một bình chứa nước dạng như Hình 13 có chiều cao là $\frac{3\pi }{2}$ dm. Nếu lượng nước trong bình có chiều cao là x (dm) thì mặt nước là hình tròn có bán kính $\sqrt{2-\mathrm{s}\text{inx}}$(dm) với 0 ≤ x ≤ $\frac{3\pi }{2}$. Tính dung tích của hình (kết quả làm tròn đến hàng phần trăm của đềximét khối).

Lời giải:

Diện tích mặt nước hình tròn bán kính $R=\sqrt{2-\mathrm{s}\text{inx}}$(dm) là:

$S\left(x\right)=\pi R^2=\pi {\left(\sqrt{2-\mathrm{s}\text{inx}}\right)}^2=\pi .\left(2-\sin \text{x}\right)$ (dm²).

Dung tích của bình là:

$V=\underset{0}{\overset{\frac{3\pi }{2}}{\int }}S\left(x\right)dx=\underset{0}{\overset{\frac{3\pi }{2}}{\int }}\pi \left(2-\sin x\right)dx$

$={\left.\pi \left(2x+\cos x\right)\right|}_0^{\frac{3\pi }{2}}$

$=\pi \left(3\pi -1\right)\approx \mathrm{26,47}$ (dm³).

Lời giải SBT Toán 12 Bài 3: Ứng dụng hình học của tích phân hay khác:

• Bài 1 trang 20 SBT Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi. Đồ thị của hàm số y = 3x(2 – x), trục hoành với hai đường thẳng x = −1, x = 1. ....

• Bài 2 trang 20 SBT Toán 12 Tập 2: Tính diện tích của hình phẳng được gạch chéo trong mỗi hình sau. ....

• Bài 3 trang 21 SBT Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số ....

• Bài 4 trang 21 SBT Toán 12 Tập 2: Cho hàm số y = x² – 2x có đồ thị (C). Kí hiệu A là hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng x = 0, x = 2 ....

• Bài 5 trang 21 SBT Toán 12 Tập 2: Kí hiệu S(a) là diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = $\frac{3}{x^2}$, trục hoành và hai đường thẳng x = 1, x = a ....

• Bài 7 trang 21 SBT Toán 12 Tập 2: Cho D là hình phẳng giới hạn bởi đồ thị của hàm số y = 2x³, trục hoành và hai đường thẳng x = −1, x = 1 ....

• Bài 8 trang 22 SBT Toán 12 Tập 2: Gọi D là hình phẳng giới hạn bởi đồ thị của hai hàm số y = x² và y = $\sqrt{x}$ (Hình 14) ....

• Bài 9 trang 22 SBT Toán 12 Tập 2: Mặt cắt ngang của lòng máng dẫn nước là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như Hình 15 ....

• Bài 10 trang 22 SBT Toán 12 Tập 2: Một bể cá có dạng là một phần hình cầu được tạo thành khi cắt hình cầu bán kính 2 dm bằng mặt phẳng cách tâm ....