Cho tam giác ABC vuông tại đỉnh A; ba điểm M, N, P lần lượt nằm trên các cạnh BC, CA, AB

Giải SBT Toán 7 Kết nối tri thức Bài tập ôn tập cuối năm

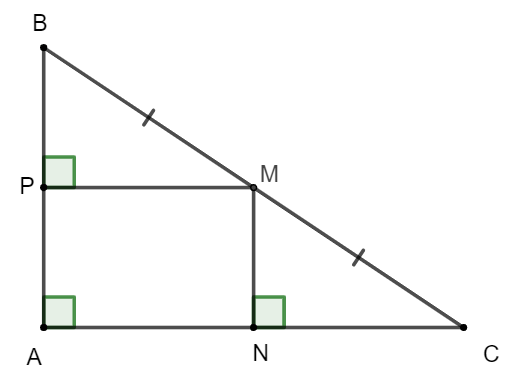
Bài 12 trang 70 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại đỉnh A; ba điểm M, N, P lần lượt nằm trên các cạnh BC, CA, AB của tam giác ABC sao cho M là trung điểm của BC, MN vuông góc với AC và MP vuông góc với AB. Chứng minh rằng:

a) ΔMNC = ΔBPM.

b) $\widehat{NMP}={90}^o$.

Lời giải:

a) Ta có :

MP ⊥ AB (gt);

AC ⊥ AB (ΔABC vuông tại A).

Suy ra MP // AC

Do đó $\widehat{BMP}=\widehat{MCN}$(hai góc so le trong).

Xét ΔBPM vuông tại P và ΔMNC vuông tại N có :

BM = MC( M là trung điểm của BC);

$\widehat{BMP}=\widehat{MCN}$(cmt).

Do đó ΔBPM = ΔMNC ( cạnh huyền – góc nhọn).

b) Ta có :

$\widehat{PBM}=\widehat{NMC}$(ΔBPM = Δ MNC, hai góc tương ứng);

$\widehat{PBM}+\widehat{PMB}={90}^o$(ΔBMP vuông tại P).

Suy ra $\widehat{NMC}+\widehat{PMB}={90}^o$.

Mà $\widehat{NMC}+\widehat{PMB}+\widehat{NMP}={180}^o$.

Do đó $\widehat{NMP}={180}^o-{90}^o={90}^o$.