Tròn đưa cho Vuông một tờ giấy, trên đó có vẽ điểm C và hai đường thẳng a và b không đi qua C

Giải SBT Toán 7 Kết nối tri thức Bài tập ôn tập cuối năm

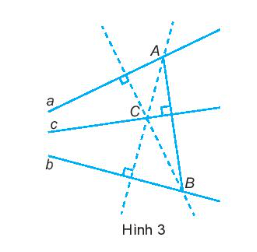
Bài 14 trang 70 sách bài tập Toán lớp 7 Tập 2: Tròn đưa cho Vuông một tờ giấy, trên đó có vẽ điểm C và hai đường thẳng a và b không đi qua C, cho biết hai đường thẳng a và b không song song với nhau (giao điểm của a và b nằm ngoài tờ giấy). Tròn đố Vuông vẽ được đường thẳng c đi qua C sao cho ba đường thẳng a, b, c đồng quy. Sau một hồi suy nghĩ, Vuông làm như sau (H.3):

- Vẽ đường thẳng đi qua C và vuông góc với a. Đường thẳng này cắt b tại B.

- Vẽ đường thẳng đi qua C và vuông góc với b. Đường thẳng này cắt a tại A.

Vuông khẳng định rằng đường thẳng c cần vẽ chính là đường thẳng đi qua C và vuông góc với AB.

Em hãy giải thích tại sao Vuông lại khẳng định như vậy.

Lời giải:

Xét tam giác ABC ta có :

a là đường cao (vì a ⊥ BC);

b là đường cao (vì b ⊥ AC);

c là đường cao (vì c ⊥ AB).

Suy ra ba đường thẳng a, b, c đồng quy (tính chất ba đường cao trong tam giác).

Vì thế Vuông khẳng định rằng đường thẳng c cần vẽ chính là đường thẳng đi qua C và vuông góc với AB là đúng.