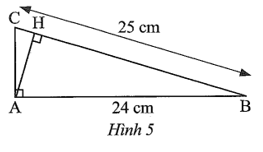
Tam giác ABC vuông tại A , có AB = 24 cm, BC = 25 cm, AH là đường cao Hình 5

Tam giác ABC vuông tại A , có AB = 24 cm, BC = 25 cm, AH là đường cao (Hình 5).

Giải sách bài tập Toán 9 Bài tập cuối chương 4 - Chân trời sáng tạo

Bài 11 trang 74 sách bài tập Toán 9 Tập 1: Tam giác ABC vuông tại A , có AB = 24 cm, BC = 25 cm, AH là đường cao (Hình 5).

Lời giải:

a) AC = 8 cm.

b) $\hat{B} \approx 16,26 ° .$

c) $\cos C = \frac{24}{25} .$

d) AH ≈ 7 cm.

Lời giải

– Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có:

BC² = AB² + AC²

Suy ra $A C = \sqrt{B C^{2} - A B^{2}} = \sqrt{25^{2} - 24^{2}} = \sqrt{625 - 576} = \sqrt{49} = 7 (cm).$

Do đó ý a) là sai.

– Xét tam giác ABC vuông tại A, ta có:

⦁ $\sin B = \frac{A C}{B C} = \frac{7}{25},$ suy ra $\hat{B} \approx 16,26 ° .$ Do đó, ý b) là đúng.

⦁ $\cos C = \frac{A C}{B C} = \frac{7}{25} .$ Do đó ý c) là sai.

– Xét tam giác ABH vuông tại H, ta có: $\sin B = \frac{A H}{A B} .$

Mà $\sin B = \frac{7}{25},$ nên $\frac{A H}{A B} = \frac{7}{25}$

Suy ra $A H = \frac{7}{25} A B = \frac{7}{25} \cdot 24 = 6,72 (cm) \approx 7 (cm).$ Do đó ý d) là đúng.

Vậy: a) S;

b) Đ;

c) S;

d) Ð.

Lời giải SBT Toán 9 Bài tập cuối chương 4 hay khác: