Cho hình thang cân ABCD có AB // CD. Chứng minh ABCD là tứ giác nội tiếp

Cho hình thang cân ABCD có AB // CD. Chứng minh ABCD là tứ giác nội tiếp.

Giải sách bài tập Toán 9 Bài tập cuối chương 9 - Chân trời sáng tạo

Bài 14 trang 89 sách bài tập Toán 9 Tập 2: Cho hình thang cân ABCD có AB // CD. Chứng minh ABCD là tứ giác nội tiếp.

Lời giải:

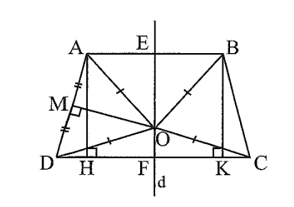
⦁ Từ A, B lần lượt kẻ AH, BK vuông góc với CD (H, K ∈ CD).

Ta có AH ⊥ CD, AB // CD nên AH ⊥ AB.

Xét ∆AHD và ∆BKC có:

$\hat{A H D} = \hat{B K C} = 90 °,$ AD = BC và $\hat{A D H} = \hat{B C K}$ (do ABCD là hình thang cân)

Do đó ∆ADH = ∆BCK (cạnh huyền – góc nhọn)

Suy ra DH = CK (hai cạnh tương ứng).

⦁ Xét tứ giác ABKH có: $\hat{A H K} = \hat{B K H} = \hat{H A B} = 90 °$ nên ABKH là hình chữ nhật.

Gọi E, F lần lượt là trung điểm của AB và HK.

Suy ra EF là đường trung trực của AB và HK.

Ta có DH = CK và HF = KF nên DF = CF, do đó F là trung điểm của DC.

Suy ra EF cũng là đường trung trực của CD.

⦁ Gọi M là trung điểm của AD. Vẽ đường trung trực MO của AD, MO cắt EF tại O.

Khi đó, O nằm trên đường trung trực của AB, AD, DC nên OA = OB, OA = OD, OD = OC

Suy ra OA = OB = OC = OD hay A, B, C, D cùng thuộc đường tròn (O; OA).

Vậy hình thang cân ABCD nội tiếp đường tròn (O; OA).

Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác: