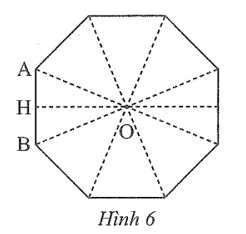
Cho bát giác đều có tâm O và AB là một cạnh, OH là đoạn vuông góc kẻ từ O đến AB
Cho bát giác đều có tâm O và AB là một cạnh, OH là đoạn vuông góc kẻ từ O đến AB.
Giải sách bài tập Toán 9 Bài tập cuối chương 9 - Chân trời sáng tạo
Câu 12 trang 89 sách bài tập Toán 9 Tập 2: Cho bát giác đều có tâm O và AB là một cạnh, OH là đoạn vuông góc kẻ từ O đến AB.
a)
b) OH = OA.sin 45°.
c) Phép quay 90° tâm O biến bát giác đều thành chính nó.
d) AB = 2OA.sin 22,5°.
Lời giải:
⦁ Ta có bát giác đều nội tiếp đường tròn (O; OA) và chia đường tròn này thành 8 cung có số đo bằng nhau, suy ra
Do đó ý a) là sai.
⦁ Ta có ∆OAB cân tại O (do OA = OB) nên
Xét ∆OAH vuông tại H, ta có:
Do đó ý b) là sai.
⦁ Các phép quay biến bát giác đều thành chính nó là các phép quay 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360° tâm O cùng chiều và ngược chiều kim đồng hồ.
Do đó ý c) là đúng.
⦁ Xét ∆OAB cân tại O có OH là đường cao nên đồng thời là đường phân giác và đường trung tuyến của tam giác.
Suy ra và H là trung điểm của AB nên AB = 2AH.
∆OAH vuông tại H, ta có:
Suy ra AB = 2OA.sin22,5°. Do đó ý d) là đúng.
Vậy:
a) S;
b) S;
c) Đ;
d) Đ.
Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác:
Câu 5 trang 87 sách bài tập Toán 9 Tập 2: Số đo của trong Hình 1 là...
Câu 7 trang 88 sách bài tập Toán 9 Tập 2: Số đo của trong Hình 3 là...