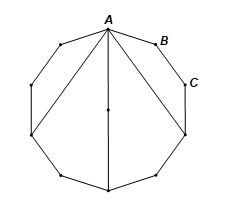
Gọi A, B, C là ba đỉnh liên tiếp của một đa giác đều có 10 cạnh. Số đo của góc ABC là

Gọi A, B, C là ba đỉnh liên tiếp của một đa giác đều có 10 cạnh. Số đo của là

Giải sách bài tập Toán 9 Bài tập cuối chương 9 - Chân trời sáng tạo

Câu 8 trang 88 sách bài tập Toán 9 Tập 2: Gọi A, B, C là ba đỉnh liên tiếp của một đa giác đều có 10 cạnh. Số đo của $\hat{A B C}$ là

A. 144°.

B. 36°.

C. 72°.

D. 152°.

Lời giải:

Đáp án đúng là: A

Gọi A, B, C là ba đỉnh liên tiếp của một đa giác đều có 10 cạnh. Số đo của góc ABC là

Ta có đa giác đều 10 cạnh là đa giác có 10 góc bằng nhau.

Tổng các góc của đa giác đều này bằng tổng các góc của 4 tứ giác và bằng: 4.360° = 1 440°.

Khi đó số đo mỗi góc của đa giác đều 10 cạnh là: $\frac{1 440 °}{10} = 144 ° .$

Do A, B, C là ba đỉnh liên tiếp của đa giác đều 10 cạnh nên $\hat{A B C}$ là một góc của đa giác đều đó, suy ra $\hat{A B C} = 144 ° .$

Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác: