Cho tam giác ABC ngoại tiếp đường tròn (I; r); D, E, F lần lượt là các tiếp điểm
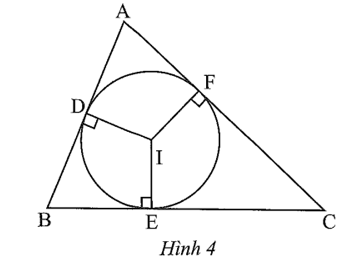
Cho tam giác ABC ngoại tiếp đường tròn (I; r); D, E, F lần lượt là các tiếp điểm của cạnh AB, BC, AC với đường tròn (I; r) (Hình 4).
Giải sách bài tập Toán 9 Bài tập cuối chương 9 - Chân trời sáng tạo
Câu 10 trang 88 sách bài tập Toán 9 Tập 2: Cho tam giác ABC ngoại tiếp đường tròn (I; r); D, E, F lần lượt là các tiếp điểm của cạnh AB, BC, AC với đường tròn (I; r) (Hình 4).
a) Ba đường trung trực của tam giác ABC cắt nhau tại I.
b) AD = AF
c) BD + CF = BC.
d) IE = r.
Lời giải:
⦁ Do tam giác ABC ngoại tiếp đường tròn (I; r) hay đường tròn (I; r) nội tiếp ∆ABC, nên ba đường phân giác của các góc A, B, C cắt nhau tại I. Do đó ý a) là sai.
⦁ Ta có D, F lần lượt là các tiếp điểm của cạnh AB, AC với đường tròn (I; r) nên AD, AF là hai tiếp tuyến của đường tròn (I; r). Suy ra AD = AF (tính chất hai tiếp tuyến cắt nhau). Do đó ý b) là đúng.
⦁ Tương tự ta cũng chứng minh được: BD = BE và CE = CF.
Suy ra BD + CF = BE + CE = BC. Do đó ý c) là đúng.
⦁ Vì D, E, F lần lượt là các tiếp điểm của cạnh AB, BC, AC với đường tròn (I; r) nên ID = IE = IF = r.
Vậy:
a) S;
b) Ð;
c) Đ;
d) Ð.
Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác:
Câu 5 trang 87 sách bài tập Toán 9 Tập 2: Số đo của trong Hình 1 là...
Câu 7 trang 88 sách bài tập Toán 9 Tập 2: Số đo của trong Hình 3 là...