Cho tam giác nhọn ABC (AB < AC) có hai đường cao BD và CE. Chứng minh bốn điểm B, C, D, E cùng thuộc một đường tròn
Cho tam giác nhọn ABC (AB < AC) có hai đường cao BD và CE. Chứng minh bốn điểm B, C, D, E cùng thuộc một đường tròn.
Giải sách bài tập Toán 9 Bài tập cuối chương 9 - Chân trời sáng tạo
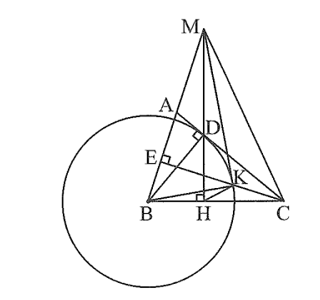
Bài 15 trang 89 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC(AB < AC) có hai đường cao BD và CE.
a) Chứng minh bốn điểm B, C, D, E cùng thuộc một đường tròn.
b) Vẽ đường tròn (B; BD). Chứng minh AC là tiếp tuyến của đường tròn (B; BD).
c) Đường tròn (B; BD) cắt CE tại K(K nằm giữa E và C). Qua D vẽ đường thẳng vuông góc với BC tại H và cắt đường thẳng AB tại M. Chứng minh
Lời giải:
a) Ta có BD ⊥ AC, CE ⊥ AB nên tam giác BEC vuông tại E và tam giác BDC vuông tại D.
∆BEC vuông tại E nên nội tiếp đường tròn đường kính BC. (1)
∆BDC vuông tại D nên nội tiếp đường tròn đường kính BC. (2)
Từ (1) và (2) suy ra bốn điểm B, C, D, E cùng thuộc đường tròn đường kính BC.
b) Ta có BD là bán kính đường tròn (B; BD) và BD ⊥ AC nên AC là tiếp tuyến của đường tròn (B; BD).
c) Xét ∆BHD và ∆BDC có:
Góc B chung;
Do đó ∆BHD ᔕ ∆BDC (g.g)
Suy ra hay BD2 = BH.BC.
Ta lại có BD = BK (bán kính đường tròn (B; BD)) nên BK2 = BH.BC.
Suy ra
Xét ∆BHK và ∆BKC có:
Góc B chung;
Do đó ∆BHK ᔕ ∆BKC (c.g.c)
Suy ra (hai góc tương ứng).
Mà (cùng phụ với nên
Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác:
Câu 5 trang 87 sách bài tập Toán 9 Tập 2: Số đo của trong Hình 1 là...
Câu 7 trang 88 sách bài tập Toán 9 Tập 2: Số đo của trong Hình 3 là...