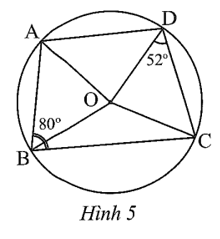
Cho tứ giác ABCD nội tiếp đường tròn (O) có góc ABC = 80 độ và góc CDO = 52 độ (Hình 5)
Cho tứ giác ABCD nội tiếp đường tròn (O) có và (Hình 5).
Giải sách bài tập Toán 9 Bài tập cuối chương 9 - Chân trời sáng tạo
Câu 11 trang 88 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O) có và (Hình 5).
a)
b)
c)
d)
Lời giải:
⦁ Vì tứ giác ABCD nội tiếp đường tròn (O) nên
Suy ra
Do đó ý a) là sai.
⦁ Xét đường tròn (O) có lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung AC, suy ra Do đó ý b) là đúng.
⦁ Ta có
Xét ∆OAD cân tại O (do OA = OD) nên
Suy ra
Do đó ý c) là đúng.
⦁ Tương tự như trên ta cũng có ∆OCD cân tại O nên
Do đó ý d) là sai.
Vậy:
a) S;
b) Đ;
c) Ð;
d) S.
Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác:
Câu 5 trang 87 sách bài tập Toán 9 Tập 2: Số đo của trong Hình 1 là...
Câu 7 trang 88 sách bài tập Toán 9 Tập 2: Số đo của trong Hình 3 là...