Cho hình bình hành ABCD tâm O. Mệnh đề nào sau đây là sai?

Câu hỏi:

A. $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$

B. $\overrightarrow{OA}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{CB}\right)$

C. $\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}+\overrightarrow{OD}$

D. $\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{DA}$

Trả lời:

Hướng dẫn giải

Đáp án đúng là: C

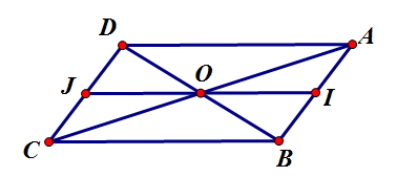
Ta xét từng đáp án:

Đáp án A: Theo quy tắc hình bình hành, ta có $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ ⇒ A đúng.

Đáp án B: Vì O là tâm của hình bình hành ABCD nên O là trung điểm AC.

Ta suy ra $OA=\frac{1}{2}CA$.

Mà $\overrightarrow{OA},\overrightarrow{CA}$ cùng hướng.

Do đó $\overrightarrow{OA}=\frac{1}{2}\overrightarrow{CA}=\frac{1}{2}\left(\overrightarrow{CB}+\overrightarrow{BA}\right)$⇒ B đúng.

Đáp án C: Gọi I, J lần lượt là trung điểm của AB và CD.

Ta có $\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OI}$ và $\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OJ}$.

Mà $\overrightarrow{OI},\overrightarrow{OJ}$ là hai vectơ đối nhau.

Do đó $2\overrightarrow{OI}\ne 2\overrightarrow{OJ}$.

Suy ra $\overrightarrow{OA}+\overrightarrow{OB}\ne \overrightarrow{OC}+\overrightarrow{OD}$ ⇒ C sai.

Đáp án D: Ta có OI là đường trung bình của tam giác ABD.

Suy ra $\overrightarrow{OI}=\frac{1}{2}\overrightarrow{DA}$.

Ta có $\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OI}=2.\frac{1}{2}\overrightarrow{DA}=\overrightarrow{DA}$ ⇒ D đúng.

Vậy ta chọn đáp án C.