Cho hình chữ nhật ABCD có AB = 4, BC = 6. M là trung điểm của BC, N là điểm trên cạnh

Câu hỏi:

A. $3\sqrt{5};$

B. $\frac{3\sqrt{5}}{2}$

C. $5\sqrt{2};$

D. $\frac{5\sqrt{2}}{2}$

Trả lời:

Hướng dẫn giải

Đáp án đúng là: D

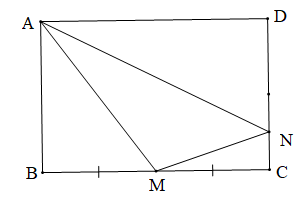
Vì M là trung điểm của BC nên BM = MC = 3.

Vì ND = 3NC nên NC = 1 và ND = 3.

Tam giác CMN vuông tại C theo định lí Py – ta – go có:

MN² = MC² + NC² = 3² + 1² = 10 $\Rightarrow MN=\sqrt{10}.$ 

Tam giác AND vuông tại D theo định lí Py – ta – go có:

AN² = AD² + DN² = 6² + 3² = 45 $\Rightarrow AN=3\sqrt{5}.$ 

Tam giác ABM vuông tại B theo định lí Py – ta – go ta có:

AM² = AB² + BM² = 4² + 3² = 25 Þ AM = 5.

Nửa chu vi của tam giác AMN là: $p=\frac{AM+AN+MN}{2}=\frac{5+3\sqrt{5}+\sqrt{10}}{2}$ 

Diện tích tam giác AMN theo công thức Heron là:

$S=\sqrt{p\left(p-AM\right)\left(p-AN\right)\left(p-MN\right)}=7,5$ (đơn vị diện tích)

Mặt khác $S=\frac{AM.AN.MN}{4R}\Rightarrow R=\frac{AM.AN.MN}{4S}$ 

$\Rightarrow R=\frac{5.3\sqrt{5}.\sqrt{10}}{4.7,5}=\frac{5\sqrt{2}}{2}.$ 

Vậy bán kính đường tròn ngoại tiếp tam giác AMN bằng $\frac{5\sqrt{2}}{2}.$