Cho hình thoi ABCD có cạnh bằng 1 cm và có đường chéo AC = căn bậc hai của 3 cm. Số đo góc BAD bằng: A. 30°; B. 45°; C. 60°; D. 120°.
Câu hỏi:
Cho hình thoi ABCD có cạnh bằng 1 cm và có đường chéo AC = \(\sqrt 3 \) cm. Số đo \(\widehat {BAD}\) bằng:
A. 30°;
B. 45°;
C. 60°;
D. 120°.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
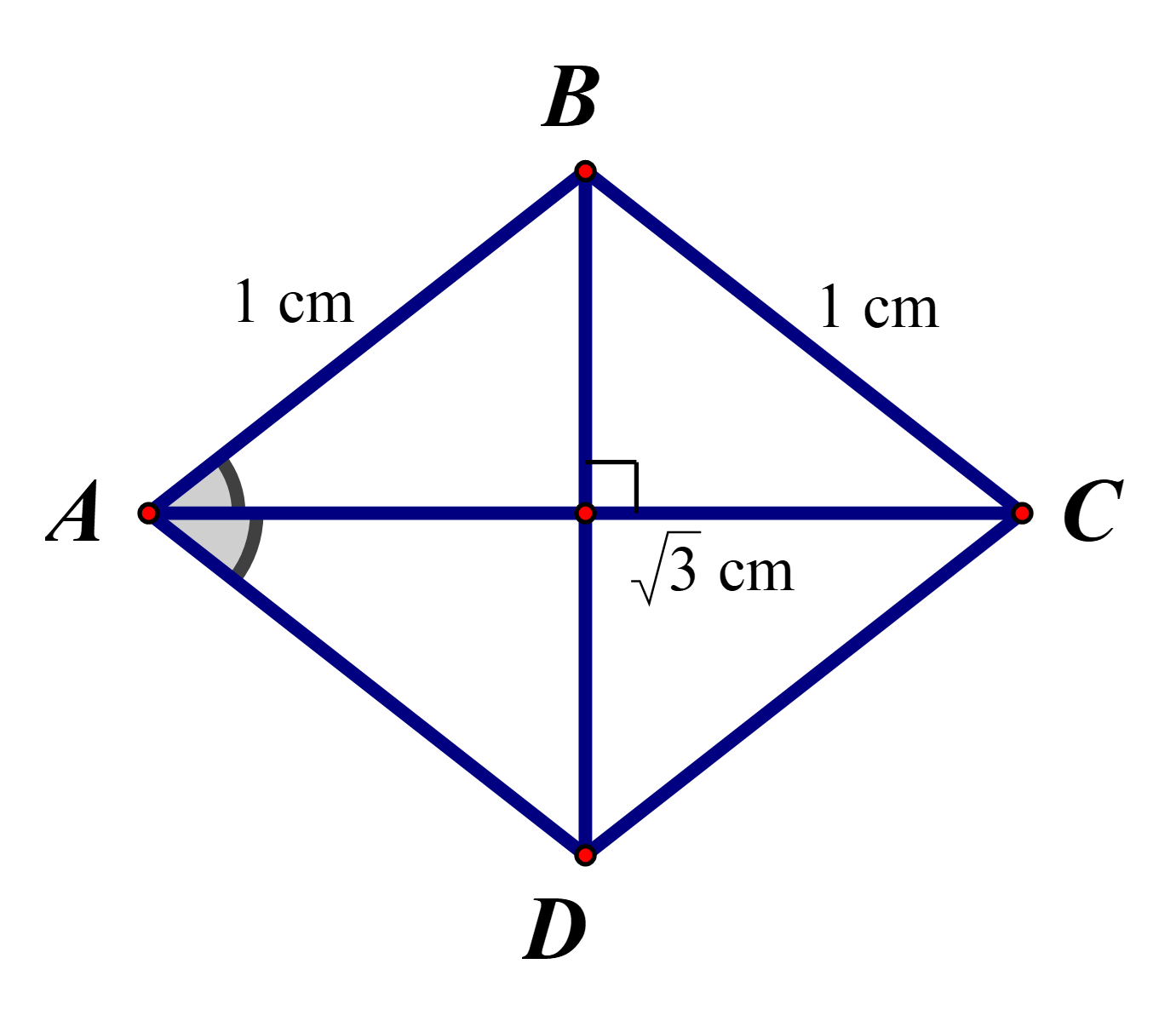
Vì ABCD là hình thoi có cạnh bằng 1 cm nên ta có AB = BC = 1 cm và AC = \(\sqrt 3 \) cm.
Áp dụng hệ quả của định lí côsin cho DABC, ta có:
\(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{1^2} + {{\left( {\sqrt 3 } \right)}^2} - {1^2}}}{{2.1.\sqrt 3 }} = \frac{{\sqrt 3 }}{2}\).
Suy ra \(\widehat {BAC} = 30^\circ \).
Vì ABCD là hình thoi nên đường chéo AC là tia phân giác của \(\widehat {BAD}\).
Suy ra \(\widehat {BAD} = 2\widehat {BAC} = 2.30^\circ = 60^\circ \).
Vậy ta chọn phương án C.
