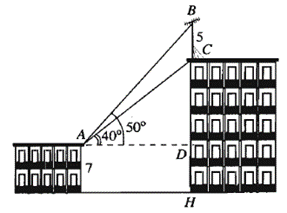
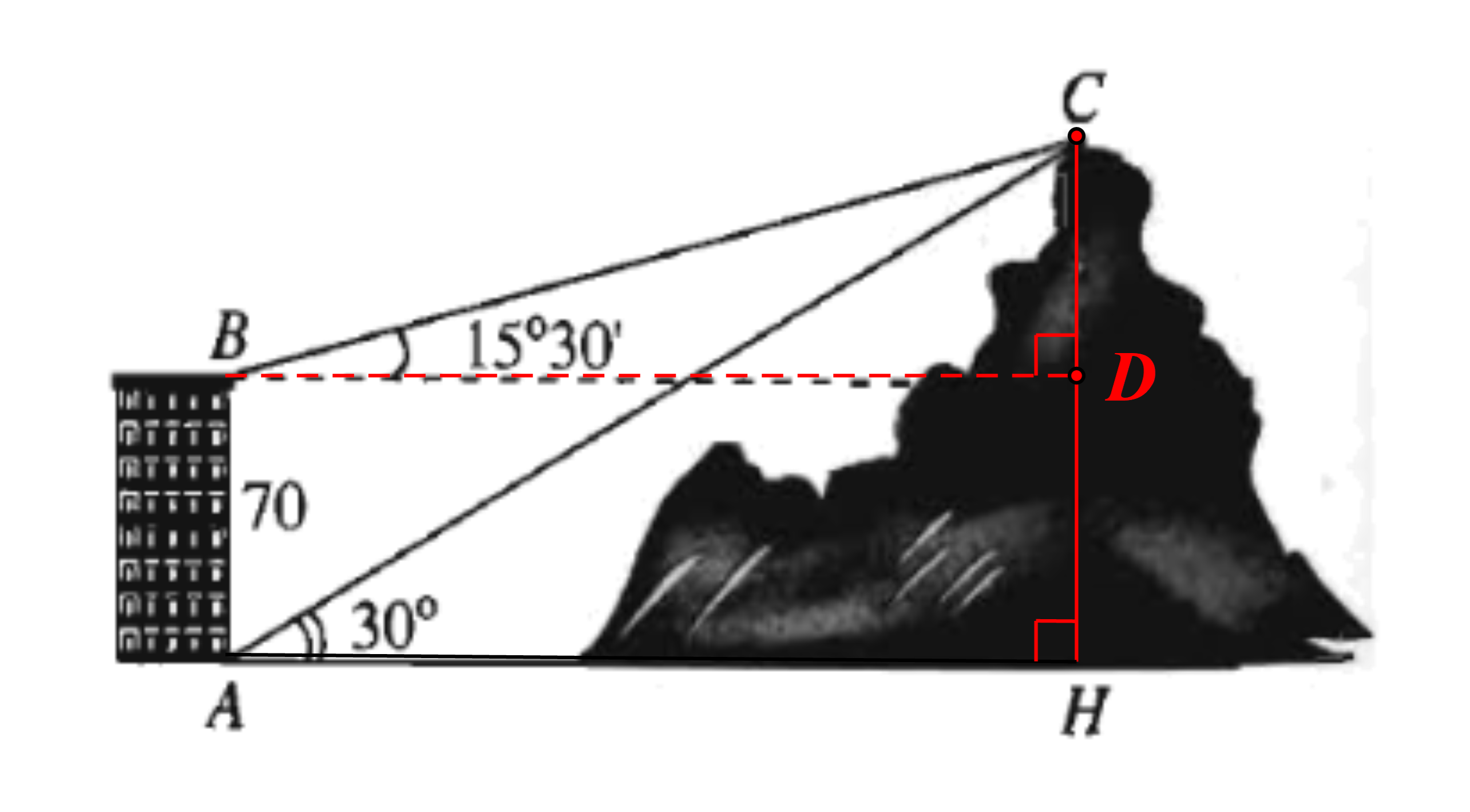
Giả sử CD = h là chiều cao của tháp, trong đó C là chân tháp. Một người đứng tại vị trí A góc CAD= 63^0, không sang được bờ bên kia để đo chiều cao h của tháp nên chọn thêm một điểm B (ba
Câu hỏi:
Giả sử CD = h là chiều cao của tháp, trong đó C là chân tháp.
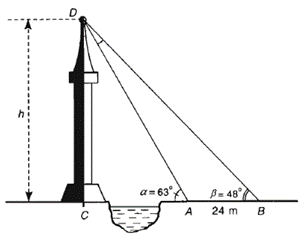
Một người đứng tại vị trí A (\(\widehat {CAD} = 63^\circ ),\) không sang được bờ bên kia để đo chiều cao h của tháp nên chọn thêm một điểm B (ba điểm A, B, C thẳng hàng) cách A một khoảng 24 m và \[\widehat {CBD} = 48^\circ \] để tính toán được chiều cao của tháp. Chiều cao h của tháp gần nhất với:
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Ta có \(\widehat {CAD} + \widehat {BAD} = 180^\circ \) (hai góc kề bù).
\( \Rightarrow \widehat {BAD} = 180^\circ - \widehat {CAD} = 180^\circ - 63^\circ = 117^\circ \).
∆ABD có: \(\widehat {BAD} + \widehat {ADB} + \widehat {ABD} = 180^\circ \) (định lí tổng ba góc trong một tam giác)
\( \Rightarrow \widehat {ADB} = 180^\circ - \left( {\widehat {BAD} + \widehat {ABD}} \right) = 180^\circ - \left( {117^\circ + 48^\circ } \right) = 15^\circ \).
Áp dụng định lí sin cho ∆ABD, ta được \(\frac{{BD}}{{\sin \widehat {BAD}}} = \frac{{AB}}{{\sin \widehat {ADB}}}\)
Suy ra \(\frac{{BD}}{{\sin 117^\circ }} = \frac{{24}}{{\sin 15^\circ }}\)
Do đó \(BD = \frac{{24.\sin 117^\circ }}{{\sin 15^\circ }} \approx 82,6\) (m)
∆BCD vuông tại C: \(\sin \widehat {CBD} = \frac{{CD}}{{BD}}\).
Suy ra \(h = CD = BD.\sin \widehat {CBD} \approx 82,6.\sin 48^\circ = 61,4\) (m)
Giá trị này gần với 60,5 m.
Vậy ta chọn phương án D.