Tam giác ABC có AB= căn bậc hai 6-2/ 2,AC= căn bậc hai 2,AC= căn bậc hai 3. Gọi D là

Câu hỏi:

Tam giác ABC có $A B = \frac{\sqrt{6} - \sqrt{2}}{2}, A C = \sqrt{2}, B C = \sqrt{3}$ . Gọi D là chân đường phân giác trong góc A. Khi đó số đo của góc ADB là:

A. 45°;

B. 60°;

C. 75°;

D. 90°.

Trả lời:

Hướng dẫn giải

Đáp án đúng là: C

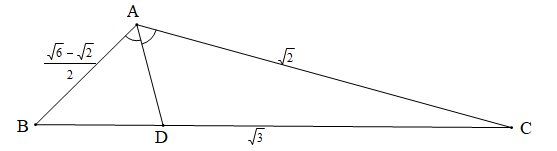
Tam giác ABC có AB= căn bậc hai 6-2/ 2,AC= căn bậc hai 2,AC= căn bậc hai 3. Gọi D là (ảnh 1)

Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:

+) $\cos \hat{A B C} = \frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C}$

$\Rightarrow \cos \hat{B A C} = \frac{{(\frac{\sqrt{6} - \sqrt{2}}{2})}^{2} + {(\sqrt{3})}^{2} - {(\sqrt{2})}^{2}}{2. (\frac{\sqrt{6} - \sqrt{2}}{2}) . \sqrt{3}} = \frac{\sqrt{2}}{2}$

$\Rightarrow \hat{A B C} = 45 °$

+) $\cos \hat{B A C} = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C}$

$\Rightarrow \cos \hat{B A C} = \frac{{(\frac{\sqrt{6} - \sqrt{2}}{2})}^{2} + {(\sqrt{2})}^{2} - {(\sqrt{3})}^{2}}{2. (\frac{\sqrt{6} - \sqrt{2}}{2}) . \sqrt{2}} = - \frac{1}{2}$

$\Rightarrow \hat{B A C} = 120 ° \Rightarrow \hat{B A D} = 60 °$ ( vì AD là tia phân giác của $\hat{B A C}$ )

Xét tam giác ABD có $\hat{B A D} = 60 °$ và $\hat{A B D} = \hat{A B C} = 45 °$ ta có:

$\hat{B A D} + \hat{A B D} + \hat{A D B} = 180 °$ (định lí tổng ba góc trong tam giác)

$\Rightarrow \hat{A D B} = 180 ° - \hat{B A D} - \hat{A B D}$

$\Rightarrow \hat{A D B} = 180 ° - 60 ° - 45 ° = 75 °$

Vậy $\hat{A D B} = 75 ° .$

Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:

Câu 1:

Giá trị của biểu thức M = tan1°.tan2°.tan3°….tan89° là:

Xem lời giải »

Câu 2:

Giá trị của biểu thức $M = \frac{\sin 60 ° + \tan 30 °}{\cot 120 ° + c o s 30 °}$ bằng:

Xem lời giải »

Câu 3:

Cho tam giác ABC có AB = 8, AC = 9, BC = 10. Tam giác ABC là tam giác:

Xem lời giải »

Câu 4:

Tam giác ABC có các góc $\hat{A} = 75 °, \hat{B} = 45 ° .$ Tỉ số $\frac{A B}{A C}$ bằng:

Xem lời giải »

Câu 5:

Tam giác có ba cạnh lần lượt là $\sqrt{3}, \sqrt{2}$ và 1. Độ dài đường cao ứng với cạnh lớn nhất là:

Xem lời giải »

Câu 6:

Tam giác ABC có góc B tù, AB = 3, AC = 4 và có diện tích bằng $3 \sqrt{3}$ . Số đo góc A là:

Xem lời giải »

Câu 7:

Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tỉ số $\frac{R}{r}$ là:

Xem lời giải »

Câu 8:

Cho hình chữ nhật ABCD có AB = 4, BC = 6. M là trung điểm của BC, N là điểm trên cạnh CD sao cho ND = 3NC. Khi đó bán kính của đường tròn ngoại tiếp tam giác AMN bằng:

Xem lời giải »

❮ Bài trước Bài sau ❯

Toán lớp 10 Chân trời sáng tạo

Tam giác ABC có AB= căn bậc hai 6-2/ 2,AC= căn bậc hai 2,AC= căn bậc hai 3. Gọi D là

Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác: