HĐ1 trang 34 Toán 10 Tập 1 - Kết nối tri thức
a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
Giải Toán lớp 10 Bài 5: Giá trị lượng giác của một góc từ 0° đến 180°
HĐ1 trang 34 Toán 10 Tập 1: a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
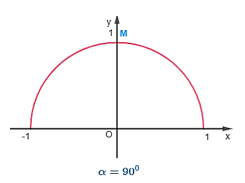
α = 90°;
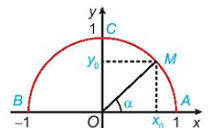
α < 90°;
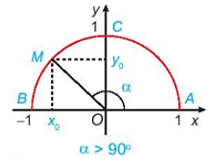
α > 90°;
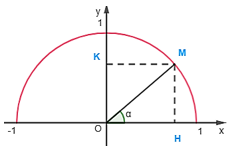
b) Khi 0° < α < 90°, nêu mối quan hệ giữa cosα, sinα với hoành độ và tung độ của điểm M.
Lời giải:
a)
Nếu α = 90° thì điểm M có tọa độ M(0;1).
Nếu α < 90° thì điểm M(x0;y0) nằm trên cung tròn (không tính điểm C) thỏa mãn 0 ≤ x0 ≤ 1, 0 ≤ y0 ≤ 1.
Nếu α > 90° thì điểm M(x0;y0) nằm trên cung tròn (không tính điểm C) thỏa mãn -1 ≤ x0 ≤ 0, 0 ≤ y0 ≤ 1.
b)
Khi 0° < α < 90° điểm M nằm ở vị trí như hình vẽ.
Kẻ MH ⊥ Ox, MK ⊥ Oy
Xét tam giác vuông MHO, có:
mà OM = 1 nên sinα = MH
Mà MH = |y0| = y0
⇒ sinα = y0
Ta lại có: mà OM = 1 nên cosα = OH
Mà OH = |x0| = x0
cosα = x0
Vậy hoành độ của điểm M bằng giá trị cosα và tung độ của điểm M bằng giá trị sinα.
Lời giải bài tập Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0° đến 180° hay, chi tiết khác:
Luyện tập 1 trang 35 Toán 10 Tập 1: Tìm các giá trị lượng giác của góc 1200 (H.3.4).
HĐ2 trang 36 Toán 10 Tập 1: Nêu nhận xét về vị trí của hai điểm M và M’ đối với trục Oy ....
Luyện tập 2 trang 36 Toán 10 Tập 1: Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau ....
Bài 3.3 trang 37 Toán 10 Tập 1: Chứng minh các hệ thức sau: a) sin2α + cos2α = 1; ....
Bài 3.4 trang 37 Toán 10 Tập 1: Cho góc α ( 00 < α < 1800) thỏa mãn tanα = 3. ....