Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3MC.
Câu hỏi:
Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3MC.
a) Tìm mối liên hệ giữa hai vecto và .
b) Biểu thị vecto theo hai vecto và
Trả lời:
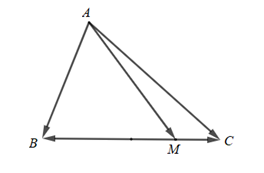
a) Vì điểm M nằm trên cạnh BC nên hai vectơ và là hai vectơ ngược hướng.
Lại có MB = 3MC nên .
Vậy
b) Theo câu a:
Ta có:
(quy tắc ba điểm)
Vậy .
Xem thêm lời giải bài tập Toán 10 Kết nối tri thức hay, chi tiết:
Câu 1:
Trong mặt phẳng tọa độ, cặp vecto nào sau đây có cùng phương?
A. và .
B. và .
C. và .
D. và .
Xem lời giải »
Câu 2:
Trong mặt phẳng tọa độ, cặp vecto nào sau đâu vuông góc với nhau?
A. và .
B. và .
C. và .
D. và .
Xem lời giải »
Câu 3:
Trong mặt phẳng tọa độ, vecto nào sau đây có độ dài bằng 1?
A.
B.
C.
D.
Xem lời giải »
Câu 4:
Góc giữa vecto và vecto có số đo bằng:
A. 900.
B. 00.
C. 1350.
D. 450.
Xem lời giải »
Câu 5:
Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:
Xem lời giải »
Câu 6:
Trong mặt phẳng tọa độ Oxy, cho A(2;1), B(-2;5) và C(-5;2).
a) Tìm tọa độ của các vecto và
b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.
Xem lời giải »
Câu 7:
Trong mặt phẳng tọa độ Oxy, cho A(1;2), B(3;4), C(-1;-2) và D(6;5)
a) Tìm tọa độ của các vecto và .
b) Hãy giải thích tại sao các vecto và cùng phương.
c) Giả sử E là điểm có tọa độ (a;1). Tìm a để vecto và cùng phương.
d) Với a tìm được, hãy biểu thị vecto theo các vecto và .
Xem lời giải »
Câu 8:
Cho vecto Chứng minh rằng (hay còn được viết là ) là một vecto đơn vị cùng hướng với .
Xem lời giải »

