Bài 2 trang 99 Toán 11 Tập 2 Cánh diều
Chứng minh: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Giải Toán 11 Bài 4: Hai mặt phẳng vuông góc - Cánh diều
Bài 2 trang 99 Toán 11 Tập 2: Chứng minh: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải:
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau.
Ta cần chứng minh rằng tồn tại một đường thẳng a nằm trong mặt phẳng (P) sao cho đường thẳng a vuông góc với mặt phẳng (Q).
Thật vậy, ta lấy:
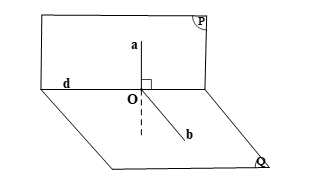
⦁ d là giao tuyến của hai mặt phẳng (P) và (Q);
⦁ a là đường thẳng nằm trong mặt phẳng (P) sao cho a ⊥ d;
· O là giao điểm của đường thẳng a và mặt phẳng (Q).
Do hai mặt phẳng (P) và (Q) cùng chứa điểm O nên hai mặt phẳng đó cắt nhau theo giao tuyến d đi qua O.
Trong mặt phẳng (Q), qua O kẻ đường thẳng b vuông góc với d.
Như vậy ta có: d là cạnh của góc nhị diện [P, d, Q];
a ⊂ (P) và a ⊥ d tại O (với O ∈ d);
b ⊂ (Q) và b ⊥ d tại O (với O ∈ d);
Suy ra là góc phẳng nhị diện của góc nhị diện [P, d, Q].
Mặt khác (P) ⊥ (Q) nên góc nhị diện [P, d, Q] vuông hay
Suy ra a ⊥ b.
Ta có: a ⊥ d, a ⊥ b và d ∩ b = O trong (Q).
Suy ra a ⊥ (Q).
Vậy nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải bài tập Toán 11 Bài 4: Hai mặt phẳng vuông góc hay, chi tiết khác: