Bài 6 trang 99 Toán 11 Tập 2 Cánh diều
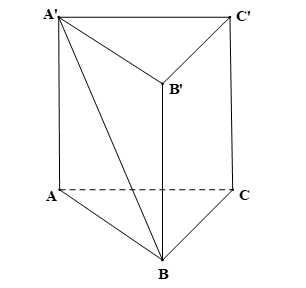
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hai mặt phẳng (A’AB) và (A’AC) cùng vuông góc với (ABC).
Giải Toán 11 Bài 4: Hai mặt phẳng vuông góc - Cánh diều
Bài 6 trang 99 Toán 11 Tập 2: Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hai mặt phẳng (A’AB) và (A’AC) cùng vuông góc với (ABC).
a) Chứng minh rằng AA’ ⊥ (ABC).
b) Tính số đo góc giữa đường thẳng A’B và mặt phẳng (ABC).
Lời giải:
a) Do A ∈ (A’AB) ∩ (A’AC) và A’ ∈ (A’AB) ∩ (A’AC).
Suy ra AA’ = (A’AB) ∩ (A’AC).
Ta có: (A’AB) ⊥ (ABC);
(A’AC) ⊥ (ABC);
(A’AB) ∩ (A’AC) = AA’.
Do đó AA’ ⊥ (ABC).
b) Do AA’ ⊥ (ABC) nên AB là hình chiếu của A’B trên (ABC).
Suy ra góc giữa đường thẳng A’B và mặt phẳng (ABC) bằng
Vì AA’ ⊥ (ABC) và AB ⊂ (ABC) nên AA’ ⊥ AB.
Xét tam giác A’AB vuông tại A có:
Vậy góc giữa đường thẳng A’B và mặt phẳng (ABC) bằng 45°.
Lời giải bài tập Toán 11 Bài 4: Hai mặt phẳng vuông góc hay, chi tiết khác: