Hoạt động 3 trang 97 Toán 11 Tập 2 Cánh diều
Cho hình chóp S.OAB thoả mãn (AOS) ⊥ (AOB), ()
Giải Toán 11 Bài 4: Hai mặt phẳng vuông góc - Cánh diều
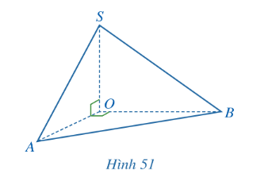
Hoạt động 3 trang 97 Toán 11 Tập 2: Cho hình chóp S.OAB thoả mãn (AOS) ⊥ (AOB), (Hình 51)
a) Giao tuyến của hai mặt phẳng (AOS) và (AOB) là đường thẳng nào?
b) SO có vuông góc với giao tuyến của hai mặt phẳng (AOS) và (AOB) hay không?
c) SO có vuông góc với mặt phẳng (AOB) hay không?
Lời giải:
a) Ta có: A ∈ (AOS) ∩ (AOB);
O ∈ (AOS) ∩ (AOB).
Suy ra AO = (AOS) ∩ (AOB).
Vậy giao tuyến của hai mặt phẳng (AOS) và (AOB) là đường thẳng AO.
b) Ta có nên SO ⊥ AO.
Mà AO là giao tuyến của hai mặt phẳng (AOS) và (AOB).
Vậy SO vuông góc với giao tuyến của hai mặt phẳng (AOS) và (AOB).
c) Vì nên AO ⊥ OB.
Ta có: AO ⊥ OB, AO ⊥ SO và OB ∩ SO = O ∈ AO.
Suy ra là góc phẳng nhị diện của góc nhị diện [S, AO, B].
Vì (AOS) ⊥ (AOB) nên
Ta có: SO ⊥ OA, SO ⊥ OB (do
OA ∩ OB = O trong (AOB).
Suy ra SO ⊥ (AOB).
Vậy SO vuông góc với mặt phẳng (AOB).
Lời giải bài tập Toán 11 Bài 4: Hai mặt phẳng vuông góc hay, chi tiết khác: