Bài 4 trang 99 Toán 11 Tập 2 Cánh diều
Cho một đường thẳng không vuông góc với mặt phẳng cho trước. Chứng minh rằng tồn tại duy nhất một mặt phẳng chứa đường thẳng đó và vuông góc với mặt phẳng đã cho.
Giải Toán 11 Bài 4: Hai mặt phẳng vuông góc - Cánh diều
Bài 4 trang 99 Toán 11 Tập 2: Cho một đường thẳng không vuông góc với mặt phẳng cho trước. Chứng minh rằng tồn tại duy nhất một mặt phẳng chứa đường thẳng đó và vuông góc với mặt phẳng đã cho.
Lời giải:
Cho đường thẳng d không vuông góc với mặt phẳng (P). Ta cần chứng minh: tồn tại duy nhất mặt phẳng (Q) vuông góc với (P) và chứa d.
Chứng minh tính tồn tại mặt phẳng (Q):
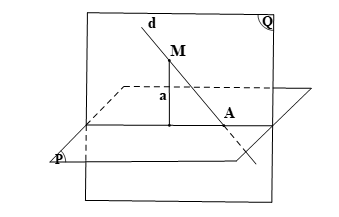
· Xét trường hợp d cắt (P) tại A.
Lấy M ∈ d sao cho M ≠ A. Vẽ đường thẳng a đi qua M sao cho a ⊥ (P).
Suy ra d ∩ a = M.
Khi đó hai đường thẳng a và d xác định mặt phẳng (Q) hay mặt phẳng (Q) chứa hai đường thẳng a và d.
Vì a ⊥ (P), a ⊂ (Q) nên ta có (P) ⊥ (Q).
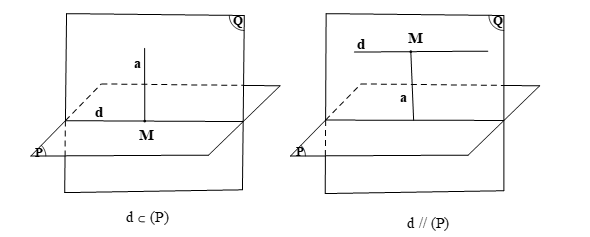
· Xét trường hợp d ⊂ (P) hoặc d // (P).
Lấy M ∈ d. Vẽ đường thẳng a đi qua M sao cho a ⊥ (P).
Suy ra d ∩ a = M.
Khi đó hai đường thẳng a và d xác định mặt phẳng (Q) hay mặt phẳng (Q) chứa hai đường thẳng a và d.
Vì a ⊥ (P), a ⊂ (Q) nên ta có (P) ⊥ (Q).
Chứng minh tính duy nhất mặt phẳng (Q):
Giả sử tồn tại mặt phẳng (Q’) khác (Q) sao cho d ⊂ (Q’) và (P) ⊥ (Q’).
Ta thấy: d = (Q’) ∩ (Q).
Mà (P) ⊥ (Q), (P) ⊥ (Q’) nên suy ra d ⊥ (P).
Mâu thuẫn với giả thiết d không vuông góc với (P).
Như vậy, tồn tại duy nhất mặt phẳng (Q) sao cho d ⊂ (Q) và (P) ⊥ (Q).
Lời giải bài tập Toán 11 Bài 4: Hai mặt phẳng vuông góc hay, chi tiết khác: