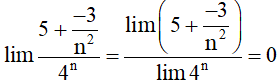Giới hạn của dãy số (Lý thuyết Toán lớp 11) | Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 11 Bài 1: Giới hạn của dãy số sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Giới hạn của dãy số (Lý thuyết Toán lớp 11) | Cánh diều

Lý thuyết Giới hạn của dãy số

1. Giới hạn hữu hạn của dãy số

1.1. Định nghĩa

– Dãy số (u_n) có giới hạn 0 khi n dần tới dương vô cực nếu |u_n| có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi, kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=0$.

– Dãy số (u_n) có giới hạn hữu hạn là a khi n dần tới dương vô cực nếu 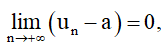 kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=a$.

Nhận xét: Nếu u_n càng ngày càng gần tới 0 khi n ngày càng lớn thì lim u_n = 0.

Chú ý:

– Ngoài kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=0$, ta cũng sử dụng kí hiệu sau:

lim u_n = 0 hay u_n → 0 khi n → +∞.

– Ngoài kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=\mathrm{a}$, ta cũng sử dụng kí hiệu sau:

lim u_n = a hay u_n → a khi n → +∞.

– Một dãy số có giới hạn thì giới hạn đó là duy nhất.

– Không phải dãy số nào cũng có giới hạn, chẳng hạn như dãy số (u_n) với u_n = (–1)ⁿ.

Ví dụ 1. Chứng minh $\lim \frac{2n+1}{n}=2$.

Hướng dẫn giải

Vì 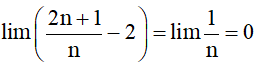 nên $\lim \frac{2n+1}{n}=2$.

2. Một số giới hạn cơ bản

Ta thừa nhận các giới hạn sau:

a) $\lim \frac{1}{n}=0$; $\lim \frac{1}{n^k}=0$ với k là số nguyên dương cho trước;

b) $\lim \frac{c}{n}=0$; $\lim \frac{\mathrm{c}}{n^k}=0$ với c là hằng số, k là số nguyên dương cho trước;

c) Nếu |q| < 1 thì lim qⁿ = 0;

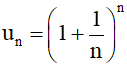
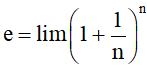
d) Dãy số (u_n) với có giới hạn là một số vô tỉ và gọi giới hạn đó là e,

.

Một giá trị gần đúng của e là 2,718281828459045.

Ví dụ 2. Chứng minh .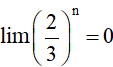

Hướng dẫn giải

.

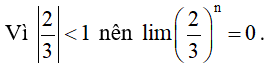
2. Định lí về giới hạn hữu hạn

a) Nếu lim u_n = a,  lim v_n = b thì:

lim (u_n + v_n) = a + b;

lim (u_n – v_n) = a – b;

lim (u_n . v_n) = a . b;

.

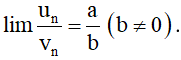
b) Nếu u_n ≥ 0 với mọi n và lim u_n = a thì a ≥ 0 và $\lim \sqrt{u_n}=\sqrt{a}$.

Ví dụ 3. Tính giới hạn của dãy số:

.

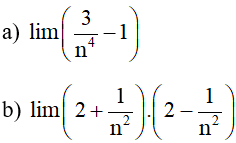
Hướng dẫn giải

.

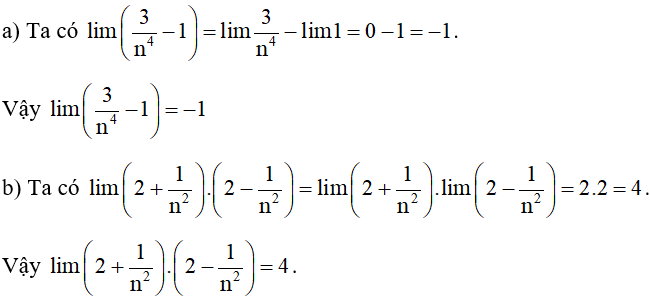
3. Tổng của cấp số nhân lùi vô hạn

Cấp số nhân vô hạn u₁, u₁q, …., u₁q^{n – 1}, … có công bội q thỏa mãn |q| < 1 được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn đã cho là:

$S=u_1+u_{1}q+\mathrm{....}+u_1{q}^{n-1}+\mathrm{...}=\frac{u_1}{1-q}$.

Ví dụ 4. Tính tổng $S=\frac{1}{3}+\frac{1}{3^2}+\mathrm{...}+\frac{1}{3^n}+\mathrm{...}$

Hướng dẫn giải

Các số hạng của tổng trên lập thành một cấp số nhân (u_n), có $u_1=\frac{1}{3}$, công bội $q=\frac{1}{3}$.

Suy ra $S=\frac{1}{3}+\frac{1}{3^2}+\mathrm{...}+\frac{1}{3^n}+\mathrm{...}=\frac{\frac{1}{3}}{1-\frac{1}{3}}=\frac{1}{2}$.

Vậy $S=\frac{1}{2}$.

4. Giới hạn vô cực

Định nghĩa dãy số có giới hạn vô cực:

– Ta nói dãy số (u_n) có giới hạn + ∞ khi n dần tới dương vô cực, nếu u_n có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

Kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=+\infty$ hay $\lim u_n=+\infty$ hay u_n → + ∞ khi n → + ∞.

– Ta nói dãy số (u_n) có giới hạn –∞ khi n dần tới dương vô cực, nếu .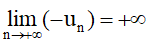

Kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=-\infty$ hay $\lim u_n=-\infty$ hay u_n → – ∞ khi n → + ∞.

Nhận xét:

• lim n^k = + ∞ với k là số nguyên dương cho trước.

• lim qⁿ = + ∞ với q > 1 là số thực cho trước.

• Nếu lim u_n = a và lim |v_n| = + ∞  thì $\lim \frac{u_n}{v_n}=0$.

• Nếu lim u_n = a, a > 0 và lim v_n = 0, v_n > 0 với mọi n  thì $\lim \frac{u_n}{v_n}=+\infty$.

• lim u_n = +∞ ⇔ lim (–u_n) = –∞.

Ví dụ 5. Chứng tỏ rằng .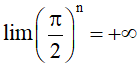

Hướng dẫn giải

Vì $\fra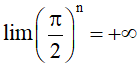c{\pi }{2}>1$ nên .

Bài tập Giới hạn của dãy số

Bài 1. Tính các giới hạn sau:

a) $\lim \frac{3}{5n-2}$;

b) $\lim \frac{-4n+6}{2n}$;

c) $\lim \frac{4^n+{6.2}^n}{{3.4}^n}$;

d) $\lim \frac{5+\frac{-3}{n^2}}{4^n}$.

Hướng dẫn giải

a) Ta có .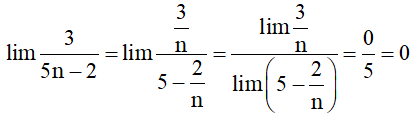

Vậy $\lim \frac{3}{5n-2}=0$.

b) Ta có .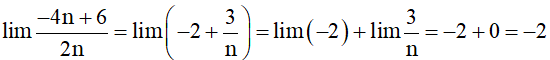

Vậy $\lim \frac{-4n+6}{2n}=-2$.

.

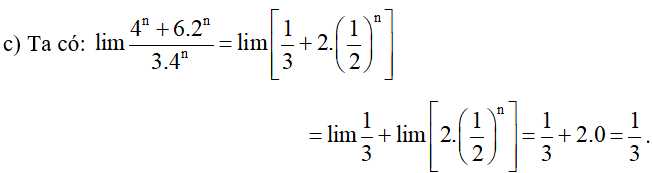
Vậy $\lim \frac{4^n+{6.2}^n}{{3.4}^n}=\frac{1}{3}$.

d) Ta có:

Vậy $\lim \frac{5+\frac{-3}{n^2}}{4^n}=0$.

Bài 2. Cho $u_n=\frac{1}{n^3}+2$ và $v_n=1-\frac{1}{n}$. Tính các giới hạn:

lim (u_n + v_n); lim(u_n – v_n); lim(u_n.v_n);  $\lim \frac{u_n}{v_n}$.

Hướng dẫn giải

.

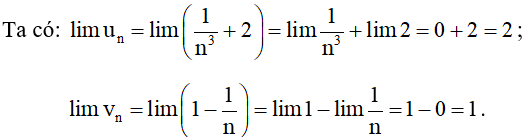
Khi đó:

• lim (u_n + v_n) = lim u_n + lim v_n = 2 + 1 = 3.

• lim (u_n – v_n) = lim u_n – lim v_n = 2 – 1 = 1.

• lim (u_n . v_n) = lim u_n . lim v_n = 2 . 1 = 2

• $\lim \frac{u_n}{v_n}=\frac{\lim u_n}{\lim v_n}=\frac{2}{1}=2$.

Bài 3. Tính tổng của cấp số nhân lùi vô hạn biết u₁ = 1, công bội $q=\frac{2}{3}$.

Hướng dẫn giải

Tổng của cấp số nhân lùi vô hạn với u₁ = 1, công bội $q=\frac{2}{3}$ là:

  $S=u_1+u_{1}q+\mathrm{...}+u_1{q}^{n-1}+\mathrm{...}=\frac{1}{1-\frac{2}{3}}=3$.

Vậy S = 3.

Học tốt Giới hạn của dãy số

Các bài học để học tốt Giới hạn của dãy số Toán lớp 11 hay khác:

• Giải sgk Toán 11 Bài 1: Giới hạn của dãy số