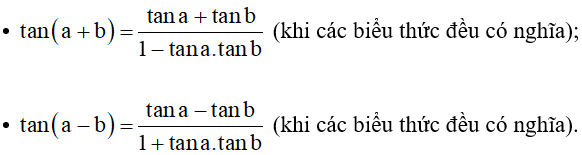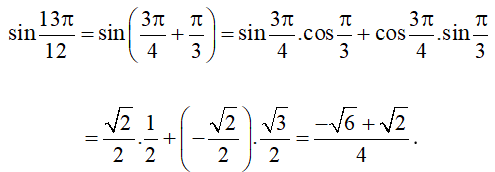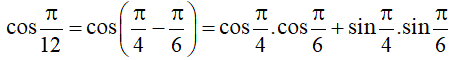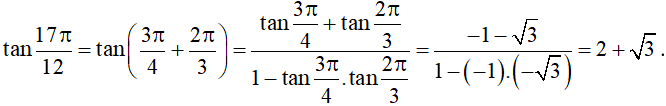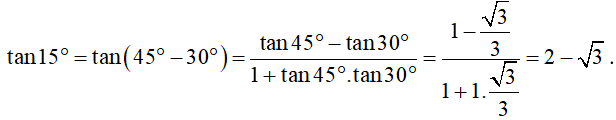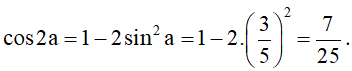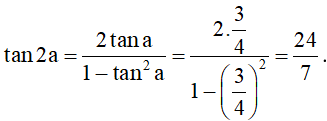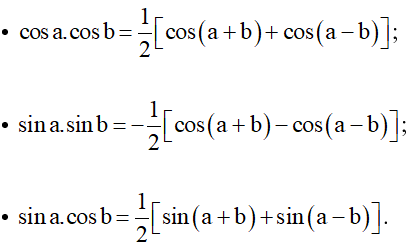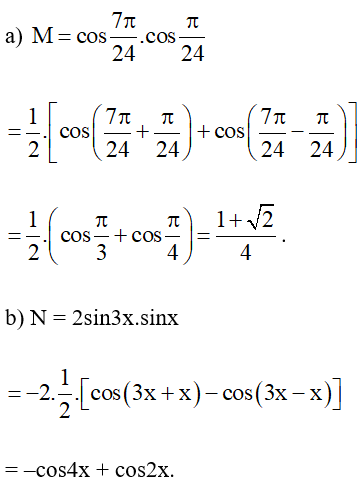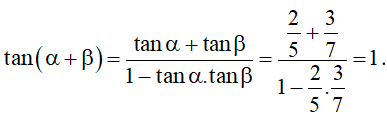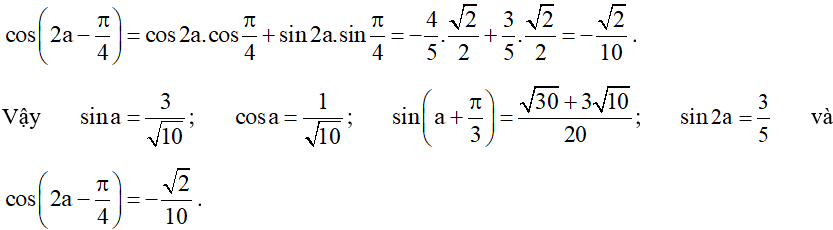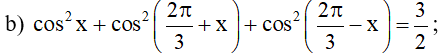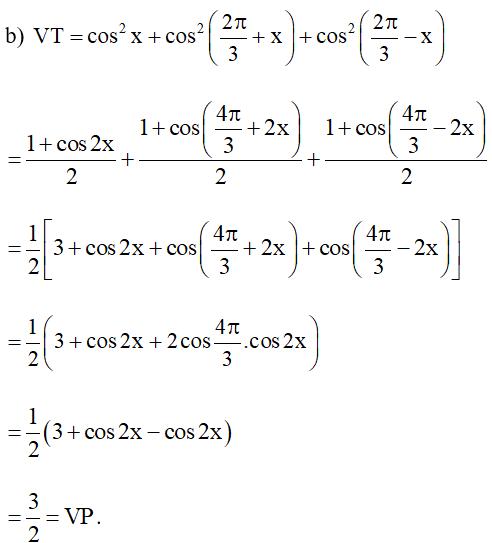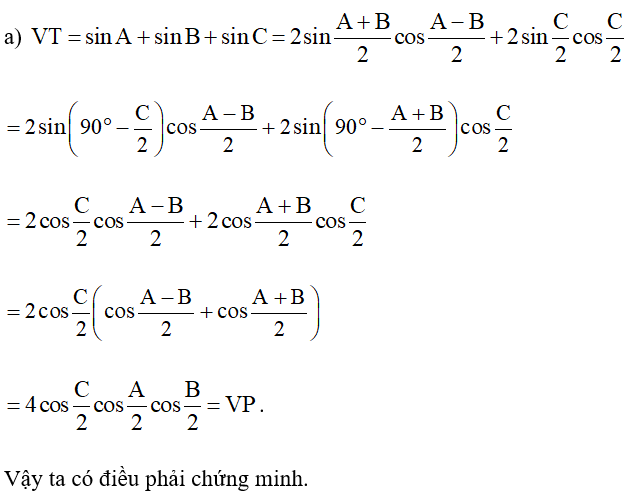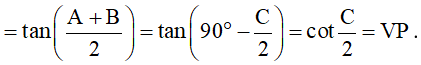Các phép biến đổi lượng giác (Lý thuyết Toán lớp 11) | Cánh diều

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 11 Bài 2: Các phép biến đổi lượng giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Các phép biến đổi lượng giác (Lý thuyết Toán lớp 11) | Cánh diều

Lý thuyết Các phép biến đổi lượng giác

1. Công thức cộng

Công thức cộng:

⦁ sin(a + b) = sina.cosb + cosa.sinb;

⦁ sin(a – b) = sina.cosb – cosa.sinb.

⦁ cos(a + b) = cosa.cosb – sina.sinb;

⦁ cos(a – b) = cosa.cosb + sina.sinb.

Ví dụ 1. Tính:

a) $\sin \frac{13\pi }{12}$;

b) sin15°.

c) cos105°;

d) $\cos \frac{\pi }{12}$.

Hướng dẫn giải

a) Áp dụng công thức cộng đối với sin, ta được:

Vậy $\sin \frac{13\pi }{12}=\frac{-\sqrt{6}+\sqrt{2}}{4}$.

b) Áp dụng công thức cộng đối với sin, ta được:

sin15° = sin(60° – 45°) = sin60°.cos45° – cos60°.sin45°

           $=\frac{\sqrt{3}}{2}.\frac{\sqrt{2}}{2}-\frac{1}{2}.\frac{\sqrt{2}}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}$.

Vậy $\sin 15°=\frac{\sqrt{6}-\sqrt{2}}{4}$.

c) Áp dụng công thức cộng đối với côsin, ta được:

cos105° = cos(60° + 45°) = cos60°.cos45° – sin60°.sin45°

             $=\frac{1}{2}.\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2}.\frac{\sqrt{2}}{2}=\frac{-\sqrt{6}+\sqrt{2}}{4}$.

Vậy $\cos 105°=\frac{-\sqrt{6}+\sqrt{2}}{4}$.

d) Áp dụng công thức cộng đối với côsin, ta được:

           $=\frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}.\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}$.

Vậy $\cos \frac{\pi }{12}=\frac{\sqrt{6}+\sqrt{2}}{4}$.

Ví dụ 2. Tính:

a) $\tan \frac{17\pi }{12}$;

b) tan15°.

Hướng dẫn giải

a) Áp dụng công thức cộng đối với tang, ta được:

Vậy $\tan \frac{17\pi }{12}=2+\sqrt{3}$.

b) Áp dụng công thức cộng đối với tang, ta được:

Vậy $\tan 15°=2-\sqrt{3}$.

2. Công thức nhân đôi

Công thức nhân đôi:

⦁ sin2a = 2sina.cosa;

⦁ cos2a = cos²a – sin²a;

⦁ $\tan 2a=\frac{2\tan a}{1-{\tan }^{2}a}$ (khi các biểu thức đều có nghĩa).

Nhận xét:

⦁ cos2a = cos²a – sin²a = 2cos²a – 1 = 1 – 2sin²a;

⦁ ${\cos }^{2}a=\frac{1+\cos 2a}{2};{\sin }^{2}a=\frac{1-\cos 2a}{2}$ (thường gọi là công thức hạ bậc).

Ví dụ 3. Cho $\sin a=\frac{3}{5}$ và $0<a<\frac{\pi }{2}$. Tính cos2a, cosa, sin2a, tan2a.

Hướng dẫn giải

• Áp dụng công thức nhân đôi, ta được:

• Vì $0<a<\frac{\pi }{2}$ nên cosa > 0.

Áp dụng công thức hạ bậc, ta được:

${\cos }^{2}a=\frac{1+\cos 2a}{2}=\frac{1+\frac{7}{25}}{2}=\frac{16}{25}$ $\iff \cos a=\frac{4}{5}$.

• Áp dụng công thức nhân đôi, ta được:

$\sin 2a=2\sin a.\cos a=2.\frac{3}{5}.\frac{4}{5}=\frac{24}{25}$.

Ta có $\tan a=\frac{\sin a}{\cos a}=\frac{3}{5}:\frac{4}{5}=\frac{3}{4}$.

• Áp dụng công thức nhân đôi, ta được:

Vậy $\cos 2a=\frac{7}{25}$; $\cos a=\frac{4}{5}$; $\sin 2a=\frac{24}{25}$ và $\tan 2a=\frac{24}{7}$.

3. Công thức biến đổi tích thành tổng

Công thức biến đổi tích thành tổng:

Ví dụ 4. Biến đổi các tích sau thành tổng:

a) $M=\cos \frac{7\pi }{24}.\cos \frac{\pi }{24}$;

b) N = 2sin3x.sinx.

Hướng dẫn giải

4. Công thức biến đổi tổng thành tích

Công thức biến đổi tổng thành tích:

⦁ $\cos u+\cos v=2.\cos \frac{u+v}{2}.\cos \frac{u-v}{2}$;

⦁ $\cos u-\cos v=-2.\sin \frac{u+v}{2}.\sin \frac{u-v}{2}$;

⦁ $\sin u+\sin v=2.\sin \frac{u+v}{2}.\cos \frac{u-v}{2}$;

⦁ $\sin u-\sin v=2.\cos \frac{u+v}{2}.\sin \frac{u-v}{2}$.

Ví dụ 5. Tính:

a) P = sinx + sin9x;

b) $Q=\frac{\cos 75°+\cos 15°}{\cos 75°-\cos 15°}$.

Hướng dẫn giải

a) P = sinx + sin9x =  sin9x + sinx

$=2\sin \frac{9x+x}{2}.\cos \frac{9x-x}{2}$

= 2sin5x.cos4x.

b) $Q=\frac{\cos 75°+\cos 15°}{\cos 75°-\cos 15°}$.

$=\frac{2\cos \frac{75°+15°}{2}.\cos \frac{75°-15°}{2}}{-2\sin \frac{75°+15°}{2}.\sin \frac{75°-15°}{2}}$

$=\frac{\cos 45°.\cos 30°}{-\sin 45°.\sin 30°}$

= –cot45°.cot30°

$=-\sqrt{3}$.

Bài tập Các phép biến đổi lượng giác

Bài 1. Tính α + β biết $\tan \alpha =\frac{2}{5},\tan \beta =\frac{3}{7}$.

Hướng dẫn giải

Áp dụng công thức cộng đối với tang, ta được:

Vậy $\alpha +\beta =\frac{\pi }{4}$.

Bài 2. Cho $\cos 2a=-\frac{4}{5}$, với $\frac{\pi }{4}<a<\frac{\pi }{2}$. Tính sina, cosa, , sin2a, .

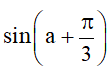
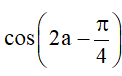
Hướng dẫn giải

Vì $\frac{\pi }{4}<a<\frac{\pi }{2}$ nên sina > 0, cosa > 0.

• Áp dụng công thức hạ bậc, ta được: ${\sin }^{2}a=\frac{1-\cos 2a}{2}=\frac{1+\frac{4}{5}}{2}=\frac{9}{10}$

Suy ra $\sin a=\frac{3}{\sqrt{10}}$ (do sina > 0)

• Áp dụng công thức hạ bậc, ta được: ${\cos }^{2}a=\frac{1+\cos 2a}{2}=\frac{1-\frac{4}{5}}{2}=\frac{1}{10}$.

Suy ra $\cos a=\frac{1}{\sqrt{10}}$.

• Áp dụng công thức cộng đối với sin, ta được:

$=\frac{3}{\sqrt{10}}.\frac{1}{2}+\frac{1}{\sqrt{10}}.\frac{\sqrt{3}}{2}=\frac{\sqrt{30}+3\sqrt{10}}{20}$.

• Áp dụng công thức nhân đôi, ta được:

$\sin 2a=2\sin a\cos a=2.\frac{3}{\sqrt{10}}.\frac{1}{\sqrt{10}}=\frac{3}{5}$.

• Áp dụng công thức cộng đối với côsin, ta được:

Bài 3. Chứng minh rằng:

a) ${\cos }^{3}x.\sin x-{\sin }^{3}x.\cos x=\frac{1}{4}\sin 4x$;

Hướng dẫn giải

a) VT = cos³x.sinx – sin³x.cosx

= cosx.sinx.(cos²x – sin²x)

$=\frac{1}{2}\sin 2x.\cos 2x$

$=\frac{1}{4}\sin 4x$ = VP.

Vậy ta có điều phải chứng minh.

Bài 4. Cho ∆ABC. Chứng minh rằng:

a) $\sin A+\sin B+\sin C=4\cos \frac{A}{2}\cos \frac{B}{2}\cos \frac{C}{2}$;

b) $\frac{\sin A+\sin B}{\cos A+\cos B}=\cot \frac{C}{2}$;

c) $\sin 2A+\sin 2B+\sin 2C=\frac{2S}{R^2}$, với R là bán kính đường tròn ngoại tiếp ∆ABC và S là diện tích ∆ABC.

Hướng dẫn giải

∆ABC, có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$, suy ra $\widehat{A}+\widehat{B}=180°-\widehat{C}$

Do đó $\frac{\widehat{A}+\widehat{B}}{2}=90°-\frac{\widehat{C}}{2}$.

b) $VT=\frac{\sin A+\sin B}{\cos A+\cos B}=\frac{2\sin \frac{A+B}{2}\cos \frac{A-B}{2}}{2\cos \frac{A+B}{2}\cos \frac{A-B}{2}}$

Vậy ta có điều phải chứng minh.

c) VT = sin2A + sin2B + sin2C

= 2sin(A + B).cos(A – B) + 2sinC.cosC

= 2sin(180° – C).cos(A – B) + 2sinC.cosC

= 2sinC.cos(A – B) + 2sinC.cosC

= 2sinC.[cos(A – B) + cosC]

= 2sinC.[cos(A – B) + cos(180° – A – B)]

= 2sinC.[cos(A – B) – cos(A + B)]

= –4sinC.sinA.sin(–B)

= 4sinA.sinB.sinC

$=4.\frac{a}{2R}.\frac{b}{2R}.\frac{c}{2R}=\frac{abc}{4R}.\frac{2}{R^2}=\frac{2S}{R^2}=VP$.

Vậy ta có điều phải chứng minh.

Học tốt Các phép biến đổi lượng giác

Các bài học để học tốt Các phép biến đổi lượng giác Toán lớp 11 hay khác:

• Giải sgk Toán 11 Bài 2: Các phép biến đổi lượng giác