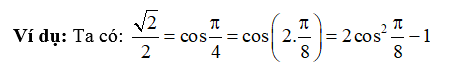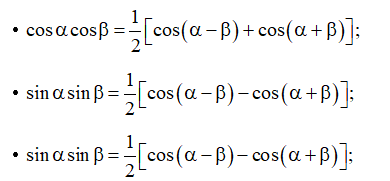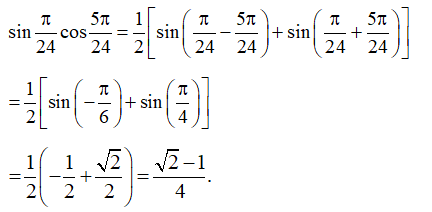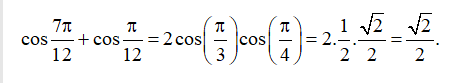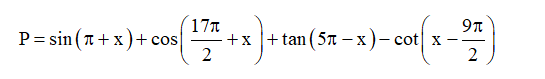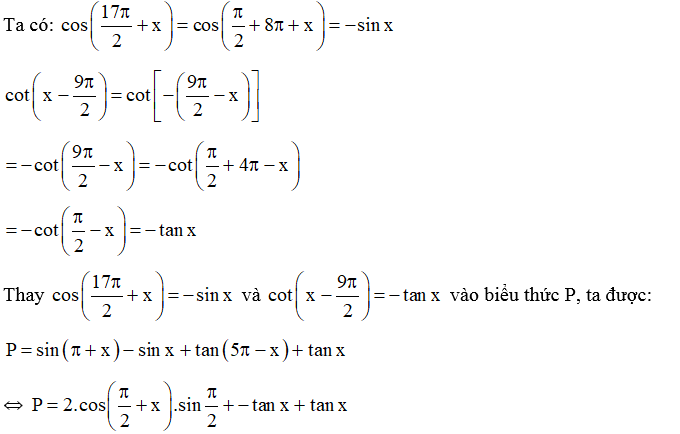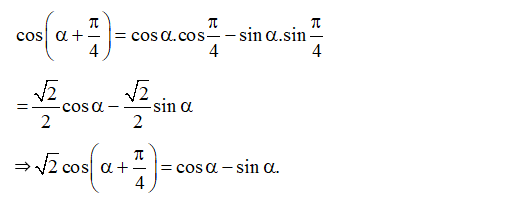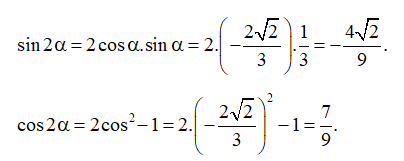Các công thức lượng giác (Lý thuyết Toán lớp 11) | Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 11 Bài 3: Các công thức lượng giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 11 dễ dàng nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Các công thức lượng giác (Lý thuyết Toán lớp 11) | Chân trời sáng tạo

Lý thuyết Các công thức lượng giác

1. Công thức cộng

• cos(α + β) = cosα.cosβ – sinα.sinβ;            

• cos(α – β) = cosα.cosβ + sinα.sinβ;

• sin(α + β) = sinα.cosβ + cosα.sinβ;             

• sin(α – β) = sinα.cosβ − cosα.sinβ;

• $\mathrm{tan(}\left(\alpha +\beta \right))=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta };$                      

• $\mathrm{tan(}\left(\alpha -\beta \right))=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }.$

$=\sin \frac{\pi }{2}\cos \frac{\pi }{3}-\cos \frac{\pi }{2}\sin \frac{\pi }{3}$

$=1.\frac{1}{2}-0.\frac{\sqrt{3}}{2}=\frac{1}{2}.$

2. Công thức góc nhân đôi

- Công thức góc nhân đôi là công thức tính các giá trị lượng giác của góc 2α qua các giá trị lượng giác của góc α.

- Công thức góc nhân đôi bao gồm những công thức sau:

• cos2α = cos²α – sin²α = 2cos²α – 1 = 1 – 2sin²α;

• sin2α = 2sinα . cosα;

• $\tan 2\alpha =\frac{2\tan \alpha }{1-{\tan }^2\alpha }.$

⇒ ${\cos }^2\frac{\pi }{8}=\frac{2+\sqrt{2}}{4}.$

Vì $0<\frac{\pi }{8}<\frac{\pi }{2}$ nên $\cos \frac{\pi }{8}>0\Rightarrow \cos \frac{\pi }{8}=\frac{\sqrt{2+\sqrt{2}}}{2}.$

3. Công thức biến đổi tích thành tổng

Ví dụ:

4. Công thức biến đổi tổng thành tích

• $\cos \alpha +\cos \beta =2\cos \frac{\alpha +\beta }{2}\cos \frac{\alpha -\beta }{2};$       

• $\cos \alpha -\cos \beta =-2\sin \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2};$

• $\sin \alpha +\sin \beta =2\sin \frac{\alpha +\beta }{2}\cos \frac{\alpha -\beta }{2};$          

• $\sin \alpha -\sin \beta =2\cos \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2}.$

Ví dụ:

Bài tập Các công thức lượng giác

Bài 1. Rút gọn biểu thức sau:

Hướng dẫn giải

⇔ $P=-2\sin x$

Vậy P = −2sin x.

Bài 2. Chứng minh rằng: $\cos \alpha -\sin \alpha =\sqrt{2}\mathrm{cos(}\left(\alpha +\frac{\pi }{4}\right)).$

Hướng dẫn giải

Ta có:

Bài 3. Cho $\sin \alpha =\frac{1}{3}$ và $\frac{\pi }{2}<\alpha <\pi .$ Tính các giá trị lượng giác của góc 2α.

Hướng dẫn giải

Do $\frac{\pi }{2}<\alpha <\pi$ ⇒ cos α < 0.

Ta có: ${\cos }^2\alpha =1-{\sin }^2\alpha =\frac{8}{9}$

⇒ $\cos \alpha =-\frac{2\sqrt{2}}{3}$ (do cos α < 0).

$\tan 2\alpha =\frac{\sin 2\alpha }{\cos 2\alpha }=-\frac{4\sqrt{2}}{9}.\frac{9}{7}=-\frac{4\sqrt{2}}{7}.$

$\cot 2\alpha =\frac{1}{\tan 2\alpha }=-\frac{7\sqrt{2}}{8}.$

Học tốt Các công thức lượng giác

Các bài học để học tốt Các công thức lượng giác Toán lớp 11 hay khác:

• Giải sgk Toán 11 Bài 3: Các công thức lượng giác