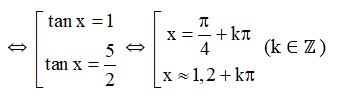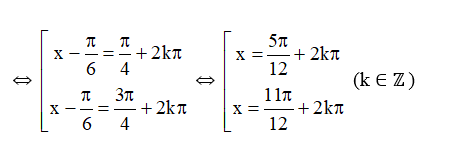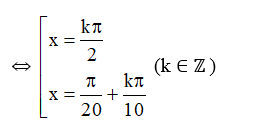Phương trình lượng giác (Lý thuyết Toán lớp 11) | Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 11 Bài 5: Phương trình lượng giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 11 dễ dàng nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Phương trình lượng giác (Lý thuyết Toán lớp 11) | Chân trời sáng tạo

Lý thuyết Phương trình lượng giác

1. Phương trình tương đương

- Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.

- Để chỉ sự tương đương của các phương trình, người ta dùng kí hiệu “⇔”.

Ví dụ: Hai phương trình x² – 9 = 0 và 3x² – 27 = 0 có cùng tập nghiệm {–3; 3} nên hai phương trình này tương đương.

2. Phương trình sin x = m

Xét phương trình sin x = m.

• Nếu |m| > 1 thì phương trình vô nghiệm.

• Nếu |m| ≤ 1 thì phương trình có nghiệm:

x = α + k2π, k ∈ ℤ

và x = π – α + k2π, k ∈ ℤ,

với α là góc thuộc [$\left[-\frac{\pi }{2};\frac{\pi }{2}\right]$] sao cho sin α = m.

Chú ý:

Một số trường hợp đặc biệt:

• sin x = 1 ⇔ $x=\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z};$              

• sin x = −1 ⇔ $x=-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z};$

• sin x = 0 ⇔ x = $k\pi ,k\in \mathbb{Z}.$

Ta có:

• sin u = sin v ⇔ u = v + k2π, k ∈ ℤ hoặc u = π – v + k2π, k ∈ ℤ.

• sin x = sin a° ⇔ x = a° + k360°, k ∈ ℤ hoặc x = 180° − a° + k360°, k ∈ ℤ.

Ví dụ: $\sin x=\frac{\sqrt{3}}{2}\iff x=\frac{\pi }{3}+k2\pi$$x=\frac{2\pi }{3}+k2\pi \left(k\in \mathbb{Z}\right).$

3. Phương trình cos x = m

Xét phương trình cos x = m.

• Nếu |m| > 1 thì phương trình vô nghiệm.

• Nếu |m| ≤ 1 thì phương trình có nghiệm:

x = α + k2π, k ∈ ℤ

và x = – α + k2π, k ∈ ℤ,

với α là góc thuộc [0; π] sao cho cos α = m.

Chú ý:

Một số trường hợp đặc biệt:

• cos x = 1 ⇔ x = k2π, k ∈ ℤ;  

• cos x = −1 ⇔ x = π + k2π, k ∈ ℤ;

• cos x = 0 ⇔ $x=\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}.$

Ta có:

• cos u = cos v ⇔ u = v + k2π, k ∈ ℤ hoặc u = –v + k2π, k ∈ ℤ.

• cos x = cos a° ⇔ x = a° + k360°, k ∈ ℤ hoặc x = −a° + k360°, k ∈ ℤ.

Ví dụ: cos x = cos 15° ⇔ x = 15° + k360° hoặc x = −15° + k360°, k ∈ ℤ.

4. Phương trình tan x = m

Với mọi số thực m, phương trình tan x = m có nghiệm

x = α + kπ, k ∈ ℤ,

với α là góc thuộc $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ sao cho tan α = m.

Chú ý: tan x = tan a° ⇔ x = a° + k180°, k ∈ ℤ.

Ví dụ: tan x = 0 ⇔ x = kπ, k ∈ ℤ.

5. Phương trình cot x = m

Với mọi số thực m, phương trình cot x = m có nghiệm

x = α + kπ, k ∈ ℤ,

với α là góc thuộc (0; π) sao cho cot α = m.

Chú ý: cot x = cot a° ⇔ x = a° + k.180°, k ∈ ℤ.

Ví dụ: cot x = 1 ⇔ $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}.$

6. Giải phương trình lượng giác bằng máy tính cầm tay

Ấn liên tiếp các phím SHIFT, sin/cos/tan và giá trị lượng giác của góc lượng giác bất kỳ để tìm ra góc lượng giác đó theo đơn vị radian hoặc theo đơn vị độ.

Chú ý: để giải phương trình cot x = m (m ≠ 0), ta giải phương trình $\tan x=\frac{1}{m}.$

Bài tập Phương trình lượng giác

Bài 1. Giải các phương trình lượng giác sau:

a) 2sin²x + 2sinx.cosx – 5cos²x = 0

b) $\sqrt{3}\sin x-\cos x=\sqrt{2}$

Hướng dẫn giải

a) $2si{n}^{2}x+2\sin x.\cos x-5co{s}^2\text{x}=0$

⇔ $2{\tan }^{2}x+3\tan x-5=0$

Vậy phương trình đã cho có nghiệm là $x=\frac{\pi }{4}+k\pi$ hoặc $x\approx 1,2+k\pi$ (k ∈ ℤ).

b) $\sqrt{3}\sin x-\cos x=\sqrt{2}$

⇔ $\frac{\sqrt{3}}{2}\sin x-\frac{1}{2}\cos x=\frac{\sqrt{2}}{2}$

⇔ $\sin x.\cos \frac{\pi }{6}-\cos x.\sin \frac{\pi }{6}=\frac{\sqrt{2}}{2}$

⇔ $\sin \left(x-\frac{\pi }{6}\right)=\sin \frac{\pi }{4}$

Vậy phương trình đã cho có nghiệm là $x=\frac{5\pi }{12}+2k\pi$ hoặc $x=\frac{11\pi }{12}+2k\pi$ (k ∈ ℤ).

Bài 2. Giải phương trình: cos3x.tan5x = sin7x.

Hướng dẫn giải

Điều kiện cos 5x ≠ 0

Khi đó phương trình đã cho trở thành

2sin5x.cos3x = 2sin7x.cos5x

⇔ sin8x = sin12x

• Với $x=\frac{k\pi }{2}$ thì ta có:

$\cos 5x=\cos \frac{5k\pi }{2}=\cos \left(\frac{k\pi }{2}+2k\pi \right)=\cos \left(\frac{k\pi }{2}\right)\ne 0$

⇔ k = 2m (m ∈ ℤ)

• Với $x=\frac{\pi }{20}+\frac{k\pi }{10}$ thì ta có:

$\cos 5x=\cos \left(\frac{\pi }{4}+\frac{k\pi }{2}\right)\ne 0$

 Vậy phương trình đã cho có nghiệm là $x=m\pi ;x=\frac{\pi }{20}+\frac{k\pi }{10}$ (m, k ∈ ℤ).

Bài 3. Tìm x ∈ [0; 14] sao cho: cos3x – 4cos2x + 3cos x – 4 = 0. (1)

Hướng dẫn giải

Ta có: cos3x = 4cos³x – 3cosx

(1) ⇔ cos3x + 3cos x – 4(1 + cos2x) = 0

⇔ 4cos³x – 8cos²x = 0

⇔ 4cos³x.(cos x – 2) = 0

⇔ cos x = 0

⇔ $x=\frac{\pi }{2}+k\pi$ (k ∈ ℤ)

Vì x ∈ [0; 14] ⇒ {$x\in \left\{\frac{\pi }{2};\frac{3\pi }{2};\frac{5\pi }{2};\frac{7\pi }{2}\right\}.$}

Vậy {$x\in \left\{\frac{\pi }{2};\frac{3\pi }{2};\frac{5\pi }{2};\frac{7\pi }{2}\right\}.$}

Học tốt Phương trình lượng giác

Các bài học để học tốt Phương trình lượng giác Toán lớp 11 hay khác:

• Giải sgk Toán 11 Bài 5: Phương trình lượng giác