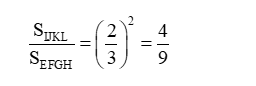Hai mặt phẳng song song (Lý thuyết Toán lớp 11) | Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 11 Bài 4: Hai mặt phẳng song song sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 11 dễ dàng nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Hai mặt phẳng song song (Lý thuyết Toán lớp 11) | Chân trời sáng tạo

Lý thuyết Hai mặt phẳng song song

1. Hai mặt phẳng song song

Cho hai mặt phẳng (P) và (Q), có thể xảy ra một trong ba trường hợp:

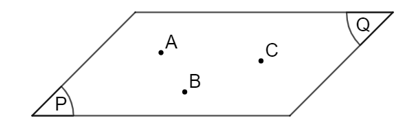
• Trường hợp 1: (P) và (Q) có ba điểm chung không thẳng hàng, ta nói hai mặt phẳng (P) và (Q) trùng nhau.

Kí hiệu: (P) = (Q)

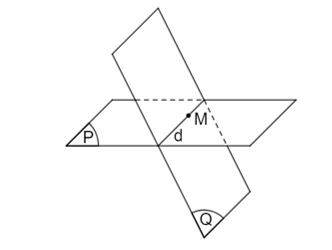
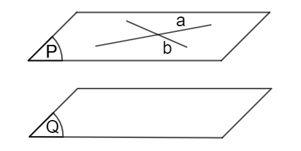
• Trường hợp 2: (P) và (Q) phân biệt và có một điểm chung, ta nói (P) và (Q) cắt nhau theo giao tuyến d đi qua điểm chung.

Kí hiệu: (P) $\cap$ (Q) = d

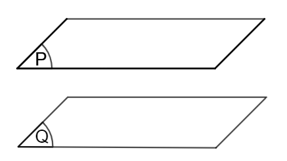
• Trường hợp 3: (P) và (Q) không có bất kì điểm chung nào, nghĩa là (P) $\cap$ (Q) = $\varnothing$, ta nói (P) và (Q) song song.

Kí hiệu: (P) // (Q) hoặc (Q) // (P)

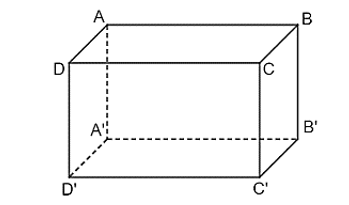
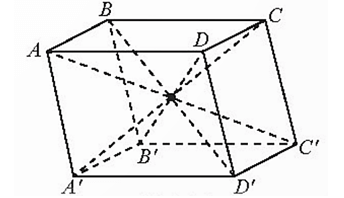
Ví dụ: Kể tên các cặp mặt phẳng song song của hình hộp chữ nhật ABCD.A’B’C’D’.

Hướng dẫn giải

Các cặp mặt phẳng song song của hình hộp chữ nhật ABCD.A’B’C’D’ là:

(ABCD) và (A’B’C’D’); (ABB’A’) và (DCC’D’); (ADD’A’) và (BCC’B’).

2. Điều kiện để hai mặt phẳng song song

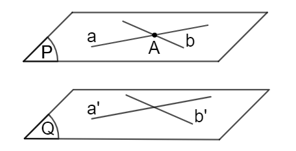
Định lí 1: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng (Q) thì (P) song song với (Q).

Chú ý: Chẳng hạn nếu A, B, C không thẳng hàng và AB // MN và AC // MP thì (ABC) // (MNP).

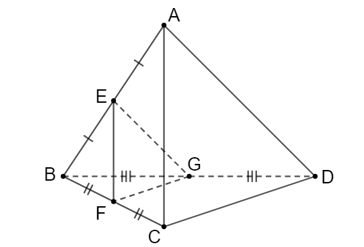
Ví dụ: Cho tứ diện ABCD. Gọi E, F và G lần lượt là trung điểm của ba cạnh AB, BC và BD. Chứng minh (EFG) // (ACD)

Hướng dẫn giải

Xét tam giác ABD có E và G lần lượt là trung điểm của BA và BD nên ta có EG là đường trung bình của tam giác ABD

Do đó EG // AD

Mà AD $\subset$ (ACD) nên suy ra EG // (ACD) (1)

Xét tam giác ABC có E và F lần lượt là trung điểm của BA và BC nên ta có EF là đường trung bình của tam giác ABC

Do đó EF // AC

Mà AC $\subset$ (ACD) nên suy ra EF // (ACD) (2)

Lại có EF $\subset$ (EFG) và EG $\subset$ (EFG) (3)

Từ (1), (2) và (3) suy ra (EFG) // (ACD).

3. Tính chất của hai mặt phẳng song song

Định lí 2: Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đó.

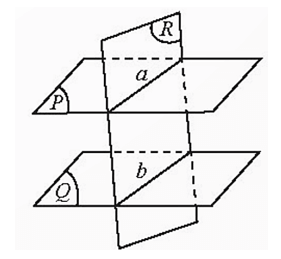
Định lí 3: Cho hai mặt phẳng (P) và (Q) song song với nhau. Nếu (R) cắt (P) thì cắt (Q) và hai giao tuyến của chúng song song với nhau.

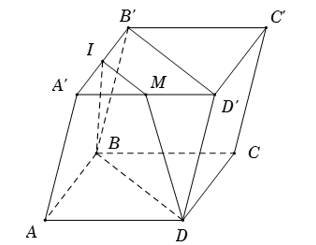
Ví dụ: Cho hình hộp ABCD.A'B'C'D'. Cho I là trung điểm của A'B'. Qua I kẻ một đường thằng song song với B'D' và cắt A'D' tại M. Tứ giác IMDB là hình gì?

Hướng dẫn giải

Theo bài ra ta có IM // B’D’.

Mà B’D’ // BD nên suy ra IM // BD

Do đó IM và BD đồng phẳng.

Mặt phẳng (IMDB) cắt hai mặt phẳng song song (ABCD) và (A’B’C’D’) theo hai giao tuyến ta là BD và IM

Do đó BD // IM

Vậy tứ giác IMDB là hình thang.

4. Định lí Thalès trong không gian

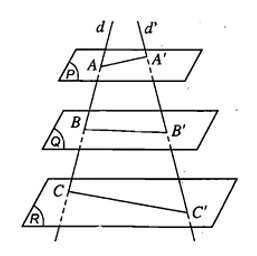
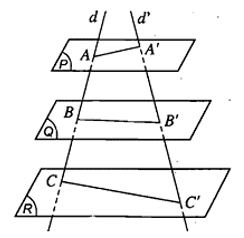
Định lí 4 (Định lí Thalès): Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ.

Ví dụ: Cho ba mặt phẳng (P), (Q), (R) đôi một song song. Hai đường phẳng d và d' cắt ba mặt phẳng (P), (Q), (R) lần lượt tại A, B, C và A', B', C'. Cho AB = 3, BC = 5, A'C' = 24. Tính các độ dài A'B'; B'C'.

Hướng dẫn giải

Áp dụng định lí Thalès trong không gian đối với ba mặt phẳng song song (P), (Q), (R) và hai cát tuyến d, d' ta có:

$\frac{A\text{'}B\text{'}}{B\text{'}C\text{'}}=\frac{AB}{BC}=\frac{3}{5}$

$\Rightarrow \frac{A\text{'}B\text{'}}{3}=\frac{B\text{'}C\text{'}}{5}=\frac{A\text{'}B\text{'}+B\text{'}C\text{'}}{3+5}=\frac{A\text{'}C\text{'}}{8}=\frac{24}{8}=3$

Do đó $A\text{'}B\text{'}=3.3=9;B\text{'}C\text{'}=3.5=15$ .

5. Hình lăng trụ và hình hộp

5.1. Hình lăng trụ

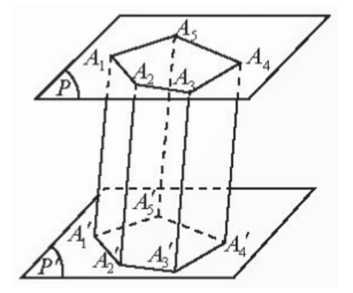
Cho hai mặt phẳng (P) và (P') song song với nhau. Trên (P) cho đa giác lồi A₁A₂…A_n. Qua các đỉnh của đa giác này, ta vẽ các đường thẳng song song với nhau và cắt (P') lần lượt tại ${A_1}^{\text{'}},{A_2}^{\text{'}},\mathrm{...},{A_n}^{\text{'}}$ .Hình tạo bởi các hình bình hành $A_1{A}_2{A_2}^{\text{'}}{A_1}^{\text{'}},\mathrm{...},A_n{A}_1{A_1}^{\text{'}}{A_n}^{\text{'}}$  và hai đa giác $A_1{A}_2\mathrm{...}{A}_n,{A_1}^{\text{'}}{A_2}^{\text{'}}\mathrm{...}{A_n}^{\text{'}}$  gọi là hình lăng trụ.

Kí hiệu: $A_1{A}_2\mathrm{...}{A}_n.{A_1}^{\text{'}}{A_2}^{\text{'}}\mathrm{...}{A_n}^{\text{'}}$

Trong hình lăng trụ $A_1{A}_2\mathrm{...}{A}_n.{A_1}^{\text{'}}{A_2}^{\text{'}}\mathrm{...}{A_n}^{\text{'}}$ , ta gọi:

- Hai đa giác A₁A₂…A_n và ${A_1}^{\text{'}}{A_2}^{\text{'}}\mathrm{...}{A_n}^{\text{'}}$  gọi là hai mặt đáy nằm trên hai mặt phẳng song song;

- Các điểm A₁, A₂, …, A_n, ${A_1}^{\text{'}},{A_2}^{\text{'}},\mathrm{...},{A_n}^{\text{'}}$  là các đỉnh;

- Các hình bình hành $A_1{A}_2{A_2}^{\text{'}}{A_1}^{\text{'}},\mathrm{...},A_n{A}_1{A_1}^{\text{'}}{A_n}^{\text{'}}$  được gọi là các mặt bên;

- Các đoạn thẳng $A_1{A_1}^{\text{'}},A_2{A_2}^{\text{'}},\mathrm{...},A_n{A_n}^{\text{'}}$  gọi là các cạnh bên. Các cạnh bên song song và bằng nhau;

- Các cạnh của hai đa giác đáy là các cạnh đáy. Các cạnh đáy tương ứng song song và bằng nhau.

Chú ý: Hình lăng trụ có đáy là tam giác, tứ giác, ngũ giác, … tương ứng được gọi là hình lăng tụ tam giác, hình lăng trụ tứ giác, hình lăng tru ngũ giác.

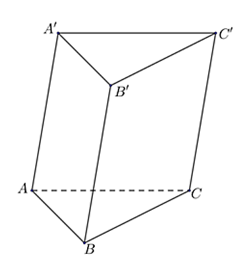
Ví dụ: Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác. Xác định các cạnh bên và mặt bên.

Hướng dẫn giải

Các cạnh bên của hình lăng trụ tam giác ABC.A'B'C' là: AA', BB', CC'

Các mặt bên của hình lăng trụ tam giác ABC.A'B'C' là: ABB'A', BCC'B', CAA'C'.

5.2. Hình hộp

Hình hộp là hình lăng trụ có đáy là hình bình hành.

Trong một hình hộp ta có:

- Sáu mặt là sáu hình bình hành. Mỗi mặt đều có một mặt song song với nó. Hai mặt như thế gọi là hai mặt đối diện;

- Hai đỉnh không cùng nằm trên một đường thẳng gọi là hai đỉnh đối diện;

- Đoạn thẳng nối hai đỉnh đối diện gọi là đường chéo;

- Bốn đường chéo cắt nhau tại trung điểm của mỗi đường.

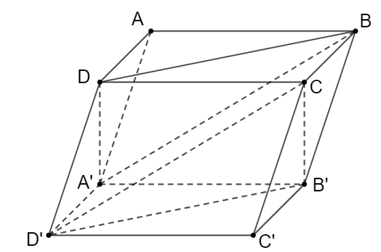
Ví dụ: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng (BDA') // (B'D'C)

Hướng dẫn giải

Xét tứ giác BDD'B' có BB' // DD' và BB' = DD' nên BDD'B' là hình bình hành

Suy ra BD // B'D'

Mà BD $\subset$ (BDA') nên suy ra B'D' // (BDA') (1)

Xét tứ giác CDA'B' có CD // AB nên CD // A'B' và CD = A'B'

Suy ra CDA'B' là hình bình hành nên A'D // B'C

Mà A'D $\subset$ (BDA') nên suy ra B'C // (BDA') (2)

Lại có B'D' $\subset$ (B'D'C) và B'C $\subset$ (B'D'C) (3)

Từ (1), (2) và (3) nên suy ra (B'D'C) // (BDA').

Bài tập Hai mặt phẳng song song

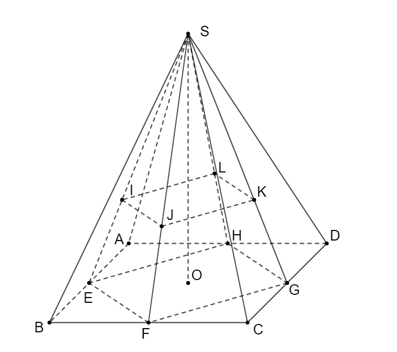
Bài 1. Cho hình chóp tứ giác đều. Gọi I, J, K, L lần lượt là các trọng tâm của các mặt bên SAB, SBC, SCD, SDA.

a) Chứng minh (IJKL) // (ABCD);

b) Giả sử ABCD có cạnh là a. Tính diện tích tứ giác IJKL.

Hướng dẫn giải

a) Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD và DA

Với I, J, K, L lần lượt là các trọng tâm của các mặt bên SAB, SBC, SCD, SDA nên ta có $\frac{SI}{SE}=\frac{SJ}{SF}=\frac{SK}{SG}=\frac{SL}{SH}=\frac{2}{3}$

Xét tam giác SEF có $\frac{SI}{SE}=\frac{SJ}{SF}$  nên suy ra IJ // EF

Mà EF $\subset$ (EFGH) $\Rightarrow$ IJ // (EFGH) (1)

Xét tam giác SEH có $\frac{SI}{SE}=\frac{SJ}{SF}$  nên suy ra IL // EH

Mà EH $\subset$ (EFGH) $\Rightarrow$ IL // (EFGH) (2)

Lại có IJ $\subset$ (IJKL) và IL $\subset$ (IJKL) (3)

Từ (1), (2) và (3) nên suy ra (IJKL) // (EFGH)

Mà (EFGH) $\subset$ (ABCD)

Do đó (IJKL) // (ABCD)

b) Với ABCD là hình vuông có cạnh là a thì diện tích hình vuông EFGH là $S_{EFGH}=\frac{1}{2}{S}_{ABCD}=\frac{1}{2}{a}^2$

Xét hình chóp S.EFGH có (IJKL) // (EFGH) và $\frac{SI}{SE}=\frac{SJ}{SF}=\frac{SK}{SG}=\frac{SL}{SH}=\frac{2}{3}$  nên suy ra 

$\Rightarrow S_{IJKL}=\frac{4}{9}{S}_{EFGH}=\frac{4}{9}\cdot \frac{1}{2}{a}^2=\frac{2}{9}{a}^2$

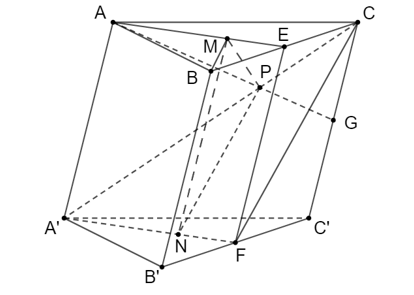
Bài 2. Cho hình lăng trụ ABC.A'B'C'. Gọi M, N, P là trọng tâm các tam giác ABC, A'B'C', ACC'. Chứng minh (MNP) // (BB'C'C).

Hướng dẫn giải

a) Gọi E, F, G lần lượt là trung điểm của ba cạnh BC, B'C' và CC'

Khi đó M là trọng tâm của tam giác ABC nên suy ra $\frac{AM}{AE}=\frac{2}{3}$

Tương tự, N và P lần lượt là trọng tâm của hai tam giác A'B'C' và tam giác ACC' nên ta có $\frac{A\text{'}N}{A\text{'}F}=\frac{2}{3};\frac{AP}{AG}=\frac{2}{3}$

Do $\frac{AM}{AE}=\frac{A\text{'}N}{A\text{'}F}=\frac{2}{3}$  nên suy ra AA' // MN // EF

Mà EF $\subset$ (BCC'B') nên suy ra MN // (BCC'B') (1)

Ta có CC' // AA' $\Rightarrow$ CG // AA'

Theo định lí Thalès thì $\frac{A\text{'}P}{PC}=\frac{AP}{PG}=2\Rightarrow \frac{A\text{'}P}{A\text{'}C}=\frac{2}{3}\Rightarrow \frac{A\text{'}P}{A\text{'}C}=\frac{A\text{'}N}{A\text{'}F}$

Do đó áp dung định lí Thalès đảo vào tam giác A'FC thì PN // CF

Mà CF $\subset$ (BCC'B') nên suy ra PN // (BCC'B') (2)

Lại có MN $\subset$ (MNP) và PN $\subset$(MNP) (3)

Từ (1), (2) và (3) nên suy ra (MPN) // (BCC'B').

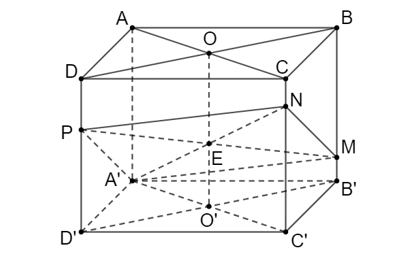
Bài 3. Cho hình hộp ABCD.A'B'C'D' có tất cả các mặt đều là hình vuông. Mặt phẳng đi qua A' cắt các cạnh BB', CC', DD' lần lượt là M, N, P. Tứ giác A'MNP là hình gì?

Hướng dẫn giải

Lấy M và P là một điểm thuộc BB' và DD'

Gọi O và O' lần lượt là tâm của hai hình vuông ABCD và A'B'C'D'

Do đó OO' $\subset$ (BDD'B') và OO' $\subset$ (ACC'A')

Gọi E là giao điểm của MP và OO' nên suy ra E $\in$ (ACC'A')

Do A'E $\subset$ (ACC'A') và A'E $\subset$ (A'MP) thì lấy N là giao điểm của A'E và CC'

Do đó A'N Ì (A'MP) và M, N, P là các điểm cần tìm

Khi đó A', M, N, P đồng phẳng

Với (AA'D'D) và (BCC'B') là hai mặt phẳng song song

Mặt phẳng (A'MNP) cắt hai mặt phẳng trên theo hai giao tuyến là A'P và MN

Nên suy ra A'P // MN (1)

Tương tự với (AA'B'B) và (DCC'D') là hai mặt phẳng song song

Mặt phẳng (A'MNP) cắt hai mặt phẳng trên theo hai giao tuyến là A'M và PN

Nên suy ra A'M // PN (2)

Từ (1) và (2) nên suy ra tứ giác A'MNP là hình bình hành.

Học tốt Hai mặt phẳng song song

Các bài học để học tốt Hai mặt phẳng song song Toán lớp 11 hay khác:

• Giải sgk Toán 11 Bài 4: Hai mặt phẳng song song