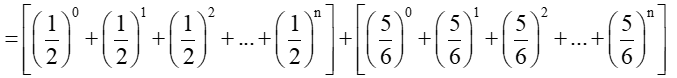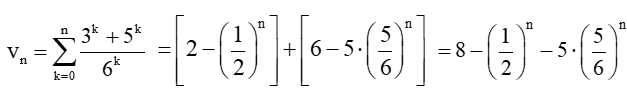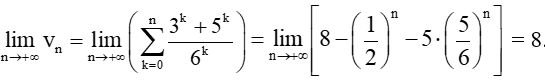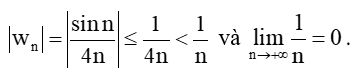Bài 5.26 trang 124 Toán 11 Tập 1 - Kết nối tri thức

Tìm giới hạn của các dãy số sau:

Giải Toán 11 Bài tập cuối Chương 5 - Kết nối tri thức

Bài 5.26 trang 124 Toán 11 Tập 1: Tìm giới hạn của các dãy số sau:

a) $u_n=\frac{n^2}{3n^2+7n-2}$;

b) $v_n=\sum _{k=0}^n\frac{3^k+5^k}{6^k}$;

c) ${\text{w}}_n=\frac{\sin n}{4n}$.

Lời giải:

a) $u_n=\frac{n^2}{3n^2+7n-2}$

Ta có: $\underset{n\to +\infty }{\lim }{u}_n=\underset{n\to +\infty }{\lim }\frac{n^2}{3n^2+7n-2}$$=\underset{n\to +\infty }{\lim }\frac{n^2}{n^2\left(3+\frac{7}{n}-\frac{2}{n^2}\right)}$$=\underset{n\to +\infty }{\lim }\frac{1}{3+\frac{7}{n}-\frac{2}{n^2}}=\frac{1}{3}$

b) $v_n=\sum _{k=0}^n\frac{3^k+5^k}{6^k}$$=\frac{3^0+5^0}{6^0}+\frac{3^1+5^1}{6^1}+\frac{3^2+5^2}{6^2}+\mathrm{...}+\frac{3^n+5^n}{6^n}$

$=\left(\frac{3^0}{6^0}+\frac{5^0}{6^0}\right)+\left(\frac{3^1}{6^1}+\frac{5^1}{6^1}\right)+\left(\frac{3^2}{6^2}+\frac{5^2}{6^2}\right)+\mathrm{...}+\left(\frac{3^n}{6^n}+\frac{5^n}{6^n}\right)$

$=\left({\left(\frac{1}{2}\right)}^0+{\left(\frac{5}{6}\right)}^0\right)+\left({\left(\frac{1}{2}\right)}^1+{\left(\frac{5}{6}\right)}^1\right)+\left({\left(\frac{1}{2}\right)}^2+{\left(\frac{5}{6}\right)}^2\right)+\mathrm{...}+\left({\left(\frac{1}{2}\right)}^n+{\left(\frac{5}{6}\right)}^n\right)$

Vì ${\left(\frac{1}{2}\right)}^1+{\left(\frac{1}{2}\right)}^2+\mathrm{...}+{\left(\frac{1}{2}\right)}^n$ là tổng n số hạng đầu của cấp số nhân với số hạng đầu là ${\left(\frac{1}{2}\right)}^1=\frac{1}{2}$ và công bội là $\frac{1}{2}$ nên

${\left(\frac{1}{2}\right)}^0+{\left(\frac{1}{2}\right)}^1+{\left(\frac{1}{2}\right)}^2+\mathrm{...}+{\left(\frac{1}{2}\right)}^n={\left(\frac{1}{2}\right)}^0+\frac{\frac{1}{2}\left(1-{\left(\frac{1}{2}\right)}^n\right)}{1-\frac{1}{2}}$$=1+\left(1-{\left(\frac{1}{2}\right)}^n\right)=2-{\left(\frac{1}{2}\right)}^n$.

Tương tự, ta tính được:

${\left(\frac{5}{6}\right)}^0+{\left(\frac{5}{6}\right)}^1+{\left(\frac{5}{6}\right)}^2+\mathrm{...}+{\left(\frac{5}{6}\right)}^n={\left(\frac{5}{6}\right)}^0+\frac{\frac{5}{6}\left(1-{\left(\frac{5}{6}\right)}^n\right)}{1-\frac{5}{6}}$$=1+5\left(1-{\left(\frac{5}{6}\right)}^n\right)=6-5\cdot {\left(\frac{5}{6}\right)}^n$.

Do đó,

Vậy

c) ${\text{w}}_n=\frac{\sin n}{4n}$

Ta có:

Do đó, $\underset{n\to +\infty }{\lim }{\text{w}}_n=\underset{n\to +\infty }{\lim }\frac{\sin n}{4n}=0$.

Lời giải bài tập Toán 11 Bài tập cuối Chương 5 hay, chi tiết khác:

• Bài 5.18 trang 123 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\sqrt{n^2+1}-\sqrt{n}$. Mệnh đề đúng là ....

• Bài 5.19 trang 123 Toán 11 Tập 1: Cho $u_n=\frac{2+2^2+\mathrm{...}+2^n}{2^n}$. Giới hạn của dãy số (u_n) bằng ....

• Bài 5.20 trang 123 Toán 11 Tập 1: Cho cấp số nhân lùi vô hạn (u_n) với $u_n=\frac{2}{3^n}.$ Tổng của cấp số nhân này bằng ....

• Bài 5.21 trang 123 Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\sqrt{x+1}-\sqrt{x+2}$. Mệnh đề đúng là ....

• Bài 5.22 trang 123 Toán 11 Tập 1: Cho hàm số f(x) ....

• Bài 5.23 trang 123 Toán 11 Tập 1: Cho hàm số f(x)....

• Bài 5.24 trang 123 Toán 11 Tập 1: Cho hàm số f(x) ....

• Bài 5.25 trang 124 Toán 11 Tập 1: Cho dãy số (un) có tính chất ....

• Bài 5.27 trang 124 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số ....

• Bài 5.28 trang 124 Toán 11 Tập 1: Tính các giới hạn sau: ....

• Bài 5.29 trang 124 Toán 11 Tập 1: Tính các giới hạn một bên: ....

• Bài 5.30 trang 124 Toán 11 Tập 1: Chứng minh rằng giới hạn ....

• Bài 5.31 trang 124 Toán 11 Tập 1: Giải thích tại sao các hàm số sau đây gián đoạn tại điểm đã cho ....

• Bài 5.32 trang 124 Toán 11 Tập 1: Lực hấp dẫn tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm Trái Đất là ....

• Bài 5.33 trang 124 Toán 11 Tập 1: Tìm tập xác định của các hàm số sau và giải thích tại sao các hàm này liên tục trên các khoảng xác định của chúng ....

• Bài 5.34 trang 124 Toán 11 Tập 1: Tìm các giá trị của a để hàm số ....