Bài 5.34 trang 124 Toán 11 Tập 1 - Kết nối tri thức

Tìm các giá trị của a để hàm số liên tục trên ℝ.

Giải Toán 11 Bài tập cuối Chương 5 - Kết nối tri thức

Bài 5.34 trang 124 Toán 11 Tập 1: Tìm các giá trị của a để hàm số liên tục trên ℝ.

Lời giải:

Ta có: 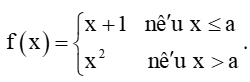Tập xác định của hàm số f(x) là ℝ.

+) Với x < a thì f(x) = x + 1 là hàm đa thức nên nó liên tục trên (–∞; a).

+) Với x > a thì f(x) = x² là hàm đa thức nên nó liên tục trên (a; +∞).

+) Tại x = a, ta có f(a) = a + 1.

$\underset{x\to a^{-}}{\lim }f\left(x\right)=\underset{x\to a^{-}}{\lim }\left(x+1\right)=a+1$; $\underset{x\to a^{+}}{\lim }f\left(x\right)=\underset{x\to a^{+}}{\lim }{x}^2=a^2$.

Để hàm số f(x) đã cho liên tục trên ℝ thì f(x) phải liên tục tại x = a, điều này xảy ra khi và chỉ khi $\underset{x\to a^{+}}{\lim }f\left(x\right)=\underset{x\to a^{-}}{\lim }f\left(x\right)=f\left(a\right)$⇔ a + 1 = a² ⇔ a² – a – 1 = 0

Suy ra $a=\frac{1-\sqrt{5}}{2}$ hoặc $a=\frac{1+\sqrt{5}}{2}$.

Vậy thì thỏa mãn yêu cầu bài toán.

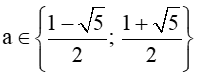
Lời giải bài tập Toán 11 Bài tập cuối Chương 5 hay, chi tiết khác:

• Bài 5.18 trang 123 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\sqrt{n^2+1}-\sqrt{n}$. Mệnh đề đúng là ....

• Bài 5.19 trang 123 Toán 11 Tập 1: Cho $u_n=\frac{2+2^2+\mathrm{...}+2^n}{2^n}$. Giới hạn của dãy số (u_n) bằng ....

• Bài 5.20 trang 123 Toán 11 Tập 1: Cho cấp số nhân lùi vô hạn (u_n) với $u_n=\frac{2}{3^n}.$ Tổng của cấp số nhân này bằng ....

• Bài 5.21 trang 123 Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\sqrt{x+1}-\sqrt{x+2}$. Mệnh đề đúng là ....

• Bài 5.22 trang 123 Toán 11 Tập 1: Cho hàm số f(x) ....

• Bài 5.23 trang 123 Toán 11 Tập 1: Cho hàm số f(x)....

• Bài 5.24 trang 123 Toán 11 Tập 1: Cho hàm số f(x) ....

• Bài 5.25 trang 124 Toán 11 Tập 1: Cho dãy số (un) có tính chất ....

• Bài 5.26 trang 124 Toán 11 Tập 1: Tìm giới hạn của các dãy số sau: ....

• Bài 5.27 trang 124 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số ....

• Bài 5.28 trang 124 Toán 11 Tập 1: Tính các giới hạn sau: ....

• Bài 5.29 trang 124 Toán 11 Tập 1: Tính các giới hạn một bên: ....

• Bài 5.30 trang 124 Toán 11 Tập 1: Chứng minh rằng giới hạn ....

• Bài 5.31 trang 124 Toán 11 Tập 1: Giải thích tại sao các hàm số sau đây gián đoạn tại điểm đã cho ....

• Bài 5.32 trang 124 Toán 11 Tập 1: Lực hấp dẫn tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm Trái Đất là ....

• Bài 5.33 trang 124 Toán 11 Tập 1: Tìm tập xác định của các hàm số sau và giải thích tại sao các hàm này liên tục trên các khoảng xác định của chúng ....