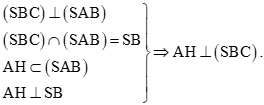Giải Toán 11 trang 56 Tập 2 Kết nối tri thức

---

Với Giải Toán 11 trang 56 Tập 2 trong Bài 26: Khoảng cách Toán lớp 11 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 56.

Giải Toán 11 trang 56 Tập 2 Kết nối tri thức

HĐ3 trang 56 Toán 11 Tập 2:

a) Cho hai đường thẳng m và n song song với nhau. Khi một điểm M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n có thay đổi hay không?

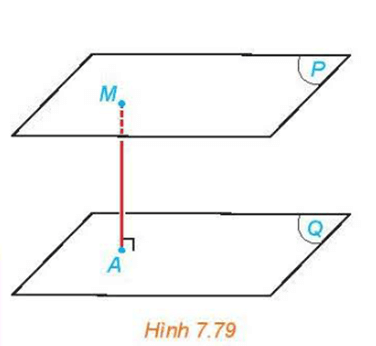
b) Cho hai mặt phẳng song song (P) và (Q) và một điểm M thay đổi trên (P) (H.7.79). Hỏi khoảng cách từ M đến (Q) thay đổi thế nào khi M thay đổi.

Lời giải:

a) Khi M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n không thay đổi vì m // n.

b) Vì (P) // (Q) nên các đường thẳng trên mặt phẳng (P) đều song song với mặt phẳng (Q).

Khi đó M thay đổi trên (P) thì khoảng cách từ M đến (Q) không thay đổi (dựa vào kết quả của hoạt động 2).

Câu hỏi trang 56 Toán 11 Tập 2: Nếu đường thẳng a thuộc mặt phẳng (P) và mặt phẳng (Q) song song với (P) thì giữa d(a, (Q)) và d((P), (Q)) có mối quan hệ gì?

Lời giải:

Lấy M bất kì thuộc a nằm trong mặt phẳng (P), suy ra M thuộc (P).

Vì a // (Q), khi đó d (a, (Q)) = d(M, (Q)).

Vì (P) // (Q) nên d((P), (Q)) = d(M, (Q)).

Do đó d(a, (Q)) = d((P), (Q)).

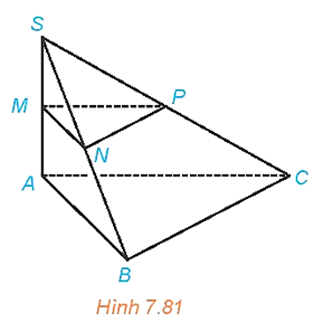
Luyện tập 2 trang 56 Toán 11 Tập 2: Cho hình chóp S.ABC có SA $\perp$ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.

a) Tính d((MNP), (ABC)) và d(NP, (ABC)).

b) Giả sử tam giác ABC vuông tại B và AB = a. Tính d(A, (SBC)).

Lời giải:

a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB nên MN là đường trung bình của tam giác SAB suy ra MN // AB, do đó MN // (ABC).

Xét tam giác SBC có N là trung điểm của SB, P là trung điểm của SC nên PN là đường trung bình của tam giác SBC suy ra PN // BC, do đó PN // (ABC).

Vì MN // (ABC) và PN // (ABC) mà MN $\cap$ PN = N nên (MNP) // (ABC).

Khi đó d((MNP), (ABC)) = d(M, (ABC)).

Vì SA $\perp$ (ABC) nên MA $\perp$ (ABC). Do đó d(M, (ABC)) = MA.

Vì M là trung điểm SA nên AM = $\frac{SA}{2}=\frac{h}{2}$ .

Do đó d((MNP), (ABC)) = $\frac{h}{2}$ .

Vì PN // (ABC) nên d(NP, (ABC)) = d(N, (ABC)).

Vì MN // (ABC) nên d(N, (ABC)) = d(M, (ABC)) = MA = $\frac{h}{2}$ .

Vậy d(NP, (ABC)) = $\frac{h}{2}$ .

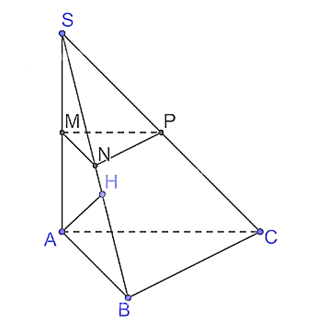
b) Vì ABC là tam giác vuông tại B nên BC $\perp$ AB.

Vì SA $\perp$ (ABC) nên SA $\perp$ BC mà BC $\perp$ AB nên BC $\perp$ (SAB), suy ra (SBC) $\perp$ (SAB).

Kẻ AH $\perp$ SB tại H.

Vì

Khi đó d(A, (SBC)) = AH.

Vì SA $\perp$ (ABC) nên SA $\perp$ AB.

Xét tam giác SAB vuông tại A, AH là đường cao, có

$\frac{1}{A{H}^2}=\frac{1}{S{A}^2}+\frac{1}{A{B}^2}=\frac{1}{h^2}+\frac{1}{a^2}=\frac{a^2+h^2}{a^2{h}^2}$$\Rightarrow AH=\frac{ah}{\sqrt{a^2+h^2}}$.

Vậy d(A, (SBC)) = $\frac{ah}{\sqrt{a^2+h^2}}$ .

Lời giải bài tập Toán 11 Bài 26: Khoảng cách Kết nối tri thức hay khác:

• Giải Toán 11 trang 55

• Giải Toán 11 trang 57

• Giải Toán 11 trang 58

• Giải Toán 11 trang 59