Bài 8 trang 58 Toán 7 Tập 2 Chân trời sáng tạo
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA
Giải Toán 7 Bài 2: Tam giác bằng nhau - Chân trời sáng tạo
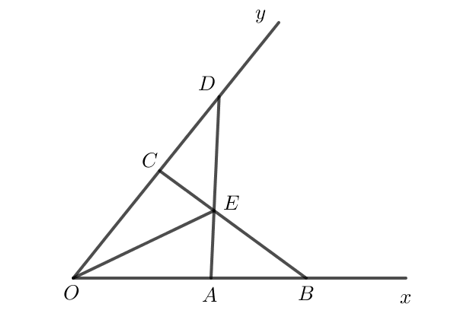
Bài 8 trang 58 Toán 7 Tập 2: Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC.
b) EAB = ECD.
c) OE là tia phân giác của góc xOy.
Lời giải:
a) Xét hai tam giác OAD và OCB có:
OA = OC (theo giả thiết).
chung.
OD = OB (theo giả thiết).
Do đó OAD = OCB (c.g.c).
Suy ra AD = BC (2 cạnh tương ứng).
b) Do OA = OC, OB = OD nên OB - OA = OD - OC hay AB = CD.
Do OAD = OCB (c.g.c) nên (2 góc tương ứng).
là góc ngoài tại đỉnh C của tam giác OBC nên (1).
là góc ngoài tại đỉnh A của tam giác OAD nên (2).
Từ (1) và (2) suy ra .
Xét hai tam giác EAB và ECD có:
(chứng minh trên).
AB = CD (chứng minh trên).
(chứng minh trên).
Do đó EAB = ECD (g.c.g).
c) Do EAB = ECD (g.c.g) nên BE = DE (2 cạnh tương ứng).
Xét hai tam giác ODE và OBE có:
OD = OB (theo giả thiết).
OE chung.
DE = BE (theo giả thiết).
Do đó ODE = OBE (c.c.c).
Suy ra (2 góc tương ứng).
Vậy OE là tia phân giác của .
Lời giải bài tập Toán 7 Bài 2: Tam giác bằng nhau hay, chi tiết khác:
Khởi động trang 48 Toán 7 Tập 2: Thế nào là hai tam giác bằng nhau? ....
Thực hành 1 trang 49 Toán 7 Tập 2: Quan sát hình 4. Hai tam giác ABC và MNP có bằng nhau không? ....