Bài 7 trang 60 Toán 9 Tập 1 Cánh diều

Cho tam giác đều ABC có độ dài cạnh là a. Tính độ dài đường cao AH của tam giác ABC theo a.

Giải Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực - Cánh diều

Bài 7 trang 60 Toán 9 Tập 1: Cho tam giác đều ABC có độ dài cạnh là a. Tính độ dài đường cao AH của tam giác ABC theo a.

Lời giải:

Xét ∆ABC đều có AH là đường cao nên đồng thời là đường trung tuyến của tam giác, do đó H là trung điểm của BC.

Suy ra HC = $\frac{B C}{2} = \frac{a}{2} .$

Xét ∆AHC vuông tại H, theo định lí Pythagore, ta có:

AC² = AH² + HC²

Suy ra AH² = AC² - HC² = a² - ${(\frac{a}{2})}^{2} = a^{2} - \frac{a^{2}}{4} = \frac{3 a^{2}}{4} .$

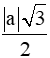
Do đó AH = $\sqrt{\frac{3 a^{2}}{4}} = \frac{\sqrt{3 a^{2}}}{\sqrt{4}}$ = Bài 7 trang 60 Toán 9 Tập 1 Cánh diều = $\frac{a \sqrt{3}}{2}$ (vì a > 0).

Vậy độ dài đường cao AH của tam giác ABC là $\frac{a \sqrt{3}}{2}$ .

Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay, chi tiết khác: