Lý thuyết Toán lớp 9 Bài 2: Tứ giác nội tiếp - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 9 Bài 2: Tứ giác nội tiếp sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán lớp 9 Bài 2: Tứ giác nội tiếp - Chân trời sáng tạo

Lý thuyết Tứ giác nội tiếp

1. Định nghĩa tứ giác nội tiếp

− Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).

− Đường tròn đi qua bốn đỉnh của tứ giác gọi là đường tròn ngoại tiếp tứ giác đó.

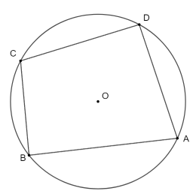
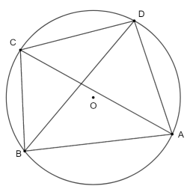
Ví dụ: Trong hình dưới đây, tứ giác ABCD nội tiếp đường tròn (O).

2. Tính chất

− Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180°.

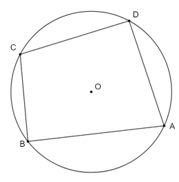
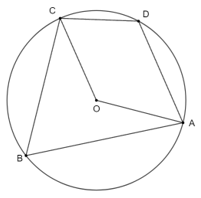
Ví dụ: Xét hình vẽ dưới đây:

Vì ABCD nội tiếp đường tròn (O) nên $\widehat{A}+\widehat{C}=180°$; $\widehat{B}+\widehat{D}=180°$.

3. Đường tròn ngoại tiếp hình chữ nhật, hình vuông

− Hình chữ nhật, hình vuông là các tứ giác nội tiếp.

− Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo.

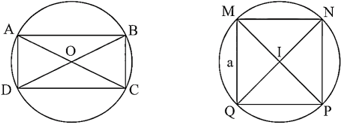
Ví dụ: Trong hình bên dưới, hình chữ nhật ABCD nội tiếp đường tròn (O) và hình vuông MNPQ nội tiếp đường tròn (I).

− Bán kính của đường tròn ngoại tiếp hình vuông cạnh a bằng $\frac{a\sqrt{2}}{2}$.

Bài tập Tứ giác nội tiếp

Bài 1. Tứ giác ABCD nội tiếp đường tròn (O) (hình 1). Chọn khẳng định sai?

A. $\widehat{BDC}=\widehat{BAC}$.

B. $\widehat{ABC}+\widehat{ADC}=180°$.

C. $\widehat{DCB}=\widehat{BAx}$.

D. $\widehat{BCA}=\widehat{BAx}$.

Hướng dẫn giải

Đáp án đúng là: D

Vì tứ giác ABCD là tứ giác nội tiếp nên:

$\widehat{BDC}=\widehat{BAC}$ (hai góc nội tiếp cùng chắn cung BC)

$\widehat{ABC}+\widehat{ADC}=180°$ (tổng hai góc đối bằng $180°$ ) 

$\widehat{DCB}=\widehat{BAx}$ (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó)

Vậy phương án A, B, C đúng.

Bài 2. Cho tứ giác ABCD nội tiếp. Chọn câu sai:

A. $\widehat{BAD}+\widehat{BCD}=180°$.

B. $\widehat{ABD}=\widehat{ACD}$.

C. $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$.

D. $\widehat{ADB}=\widehat{DAC}$.

Hướng dẫn giải

Đáp án đúng là: D

Vì tứ giác ABCD là tứ giác nội tiếp nên:

$\widehat{BAD}+\widehat{BCD}=180°$ (Tổng hai góc đối nhau)

$\widehat{ABD}=\widehat{ACD}$ (hai góc nội tiếp cùng chắn cung AD)

$\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$ (tổng 4 góc trong tứ giác)

Vậy đáp án cần chọn là D.

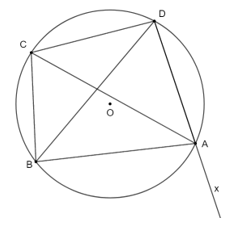
Bài 3. Trong hình vẽ dưới đây, cho $\widehat{AOC}=140°$.

a) Tính các góc $\widehat{ABC},\widehat{ADC}$ của tứ giác ABCD.

b) Tính $\widehat{BAD}+\widehat{BCD}$.

Hướng dẫn giải

a) Ta có:

$\widehat{ABC}=\frac{\widehat{AOC}}{2}=\frac{140°}{2}=70°$ (góc nội tiếp và góc ở tâm cùng chắn cung AC)

$\widehat{ABC}+\widehat{ADC}=180°$ (tứ giác ABCD nội tiếp đường tròn)

Do đó $\widehat{ADC}=180°-70°=110°.$

Vậy $\widehat{ADC}=110°$

b) Tứ giác ABCD nội tiếp đường tròn nên $\widehat{BAD}+\widehat{BCD}=180°$.

Bài 4. Cho tứ giác ABCD nội tiếp đường tròn. Tính số đo các góc còn lại của tứ giác đó trong trường hợp sau: $\widehat{A}=45°$ và $\widehat{B}=155°$.

Hướng dẫn giải

Tứ giác ABCD nội tiếp đường tròn nên $\widehat{A}+\widehat{C}=180°$; $\widehat{B}+\widehat{D}=180°$.

Do đó $\widehat{C}=180°-\widehat{A}=180°-45°=135°$;

          $\widehat{D}=180°-\widehat{B}=180°-155°=25°$.

Vậy $\widehat{C}=135°$ và $\widehat{D}=25°$.

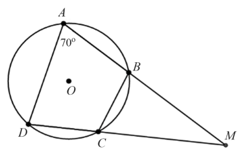
Bài 5. Tứ giác ABCD nội tiếp đường tròn có hai cạnh đối AB và CD cắt nhau tại M và $\widehat{BAD}=70°$. Tính số đo $\widehat{BCM}$.

Hướng dẫn giải

Tứ giác ABCD nội tiếp nên ta có: $\widehat{DAB}+\widehat{BCD}=180°$

Suy ra $\widehat{BCD}=180°-70°=110°$

Mà $\widehat{BCD}+\widehat{BCM}=180°$ (hai góc kề bù) nên $\widehat{BCM}=180°-110°=70°$.

Vậy $\widehat{BCM}=70°$.

Học tốt Tứ giác nội tiếp

Các bài học để học tốt Tứ giác nội tiếp Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài 2: Tứ giác nội tiếp