Giải Toán 9 trang 103 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 9 trang 103 Tập 1 trong Bài tập cuối chương 5 Toán lớp 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 103.

Giải Toán 9 trang 103 Tập 1 Chân trời sáng tạo

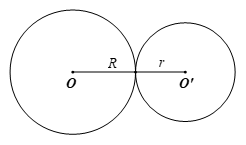
Bài 1 trang 103 Toán 9 Tập 1: Cho hai đường tròn (O; 5 cm), (O’; 4 cm) với OO’ = 9 cm. Kết luận nào sau đây đúng về vị trí tương đối của hai đường tròn?

A. Hai đường tròn cắt nhau.

B. Hai đường tròn ở ngoài nhau.

C. Hai đường tròn tiếp xúc ngoài.

D. Hai đường tròn tiếp xúc trong.

Lời giải:

Đáp án đúng là: C

Ta có: 9 = 5 + 4 nên OO’ = R + r, suy ra hai đường tròn (O; 5 cm) và (O’; 4 cm) tiếp xúc ngoài.

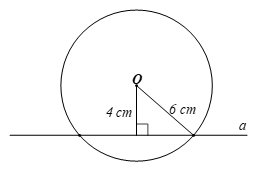
Bài 2 trang 103 Toán 9 Tập 1: Cho đường tròn (O; 6 cm) và đường thẳng a với khoảng cách từ O đến a là 4 cm. Kết luận nào sau đây đúng về vị trí giữa đường tròn (O) và đường thẳng a?

A. (O) và a cắt nhau tại hai điểm.

B. (O) và a tiếp xúc.

C. (O) và a không có điểm chung.

D. (O) và a có duy nhất điểm chung.

Lời giải:

Đáp án đúng là: A

Ta có d = 4 cm, R = 6 cm.

Vì d < R nên đường thẳng a cắt đường tròn (O; 6 cm) tại hai điểm.

Bài 3 trang 103 Toán 9 Tập 1: Góc ở tâm là góc

A. có đỉnh nằm trên đường tròn

B. có đỉnh nằm trên bán kính của đường tròn.

C. có hai cạnh là hai đường kính của đường tròn.

D. có đỉnh trùng với tâm đường tròn.

Lời giải:

Đáp án đúng là: C

Góc ở tâm là góc có đỉnh trùng với tâm đường tròn.

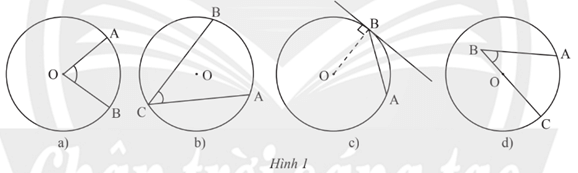
Bài 4 trang 103 Toán 9 Tập 1: Hình nào dưới đây biểu diễn góc nội tiếp?

A. Hình 1a.

B. Hình 1b.

C. Hình 1c.

D. Hình 1d.

Lời giải:

Đáp án đúng là: B

Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Vậy hình 1b là hình biểu diễn góc nội tiếp.

Bài 5 trang 103 Toán 9 Tập 1: Góc nội tiếp chắn nửa đường tròn có số đo là

A. 180°.

B. 120°.

C. 90°.

D. 60°.

Lời giải:

Đáp án đúng là: C

Góc nội tiếp chắn nửa đường tròn là góc vuông.

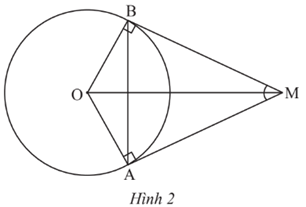
Bài 6 trang 103 Toán 9 Tập 1: Cho hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M (Hình 2).

Biết $\widehat{AMB}=50°.$ Số đo cung nhỏ AB là

A. 140°.

B. 230°.

C. 130°.

D. 150°.

Lời giải:

Đáp án đúng là: B

Xét tứ giác OAMB, ta có: $\widehat{AOB}+\widehat{OAM}+\widehat{OBM}+\widehat{AMB}=360°$ (tổng các góc của một tứ giác).

Suy ra $\widehat{AOB}=360°-\left(\widehat{OAM}+\widehat{OBM}+\widehat{AMB}\right)$

Do đó $\widehat{AOB}=360°-\left(90°+90°+50°\right)=130°.$

Khi đó $sđ\stackrel{⏜}{AB}=\widehat{AOB}=130°.$

Lời giải bài tập Toán 9 Bài tập cuối chương 5 hay khác:

• Giải Toán 9 trang 104

• Giải Toán 9 trang 105