Giải Toán 9 trang 104 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 9 trang 104 Tập 1 trong Bài tập cuối chương 5 Toán lớp 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 104.

Giải Toán 9 trang 104 Tập 1 Chân trời sáng tạo

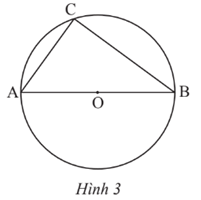
Bài 7 trang 104 Toán 9 Tập 1: Trong Hình 3, $\widehat{\text{ACB}}$ là góc

A. vuông.

B. tù.

C. nhọn.

D. bẹt.

Lời giải:

Đáp án đúng là: A

Xét đường tròn (O) đường kính AB, có $\widehat{\text{ACB}}$ là góc nội tiếp chắn nửa đường tròn nên $\widehat{\text{ACB}}=90°.$

Bài 8 trang 104 Toán 9 Tập 1: Trong một đường tròn, khẳng định nào sau đây là sai?

A. Các góc nội tiếp chắn nửa đường tròn là góc vuông.

B. Hai góc nội tiếp bằng nhau chắn hai cung bằng nhau.

C. Hai góc nội tiếp cùng chắn một cung thì bằng nhau.

D. Hai góc nội tiếp bằng nhau thì cùng chắn một cung.

Lời giải:

Đáp án đúng là: D

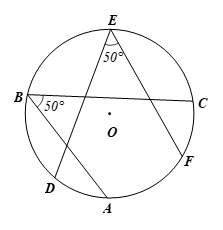
Hai góc nội tiếp bằng nhau nhưng chưa chắc đã cùng chắn một cung.

Chẳng hạn, trong hình vẽ dưới đây, $\widehat{ABC}=\widehat{DEF}=50°$ cùng là hai góc nội tiếp của đường tròn (O) nhưng hai góc này không cùng chắn một cung.

Bài 9 trang 104 Toán 9 Tập 1: Hình quạt tròn bán kính R, ứng với cung 90° có diện tích bằng

A. πR².

B. $\frac{\pi {\text{R}}^2}{2}.$

C. $\frac{\pi {\text{R}}^2}{4}.$

D. $\frac{\pi {\text{R}}^2}{8}.$

Lời giải:

Đáp án đúng là: C

Diện tích hình quạt tròn bán kính R, ứng với cung 90° là:

$S=\frac{\pi R^{2}n}{360}=\frac{\pi R^2\cdot 90}{360}=\frac{\pi R^2}{4}.$

Bài 10 trang 104 Toán 9 Tập 1: Hình vành khuyên giới hạn bởi hai đường tròn (O; 2 cm) và (O; 4 cm) có diện tích bằng

A. 12 cm².

B. 24 cm².

C. 4π cm².

D. 12π cm².

Lời giải:

Đáp án đúng là: D

Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 2 cm) và (O; 4 cm) là:

S = π(R² – r²) = π(4² – 2²) = 12π (cm²).

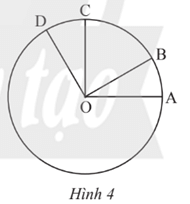
Bài 11 trang 104 Toán 9 Tập 1: Quan sát Hình 4. Biết $\widehat{DOA}=120°$, OA ⊥ OC, OB ⊥ OD.

a) Đọc tên các góc ở tâm có trong hình.

b) Tính số đo của mỗi góc ở tâm tìm được ở câu a.

c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180°.

d) So sánh hai cung nhỏ $\stackrel{⏜}{AB}$ và $\stackrel{⏜}{CD}.$

Lời giải:

a) Các góc ở tâm là: $\widehat{AOB};\widehat{AOC};\widehat{AOD};\widehat{BOC};\widehat{BOD};\widehat{COD}.$

b) Ta có: $\widehat{AOD}=\widehat{AOB}+\widehat{BOD}=\widehat{AOC}+\widehat{COD}.$ Suy ra:

⦁ $\widehat{AOB}=\widehat{AOD}-\widehat{BOD}=120°-90°=30°;$

⦁ $\widehat{COD}=\widehat{AOD}-\widehat{AOC}=120°-90°=30°.$

Ta có $\widehat{AOC}=\widehat{AOB}+\widehat{BOC}.$ Suy ra $\widehat{BOC}=\widehat{AOC}-\widehat{AOB}=90°-30°=60°.$

Vậy $\widehat{AOB}=30°;$ $\widehat{AOC}=90°;$ $\widehat{AOD}=120°;$ $\widehat{BOC}=60°;$ $\widehat{BOD}=90°;$ $\widehat{COD}=30°.$

c) Ta có:

⦁ $\widehat{AOB}=\widehat{COD}=30°$ hay $sđ\stackrel{⏜}{AB}=sđ\stackrel{⏜}{CD}$ nên $\stackrel{⏜}{AB}=\stackrel{⏜}{CD}.$

⦁ $\widehat{AOC}=\widehat{BOD}=90°$ hay $sđ\stackrel{⏜}{AC}=sđ\stackrel{⏜}{BD}$ nên $\stackrel{⏜}{AC}=\stackrel{⏜}{BD}.$

d) Ta có: $\stackrel{⏜}{AB}=\stackrel{⏜}{CD}.$

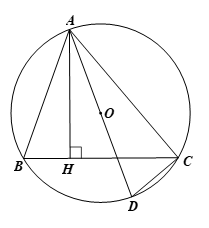
Bài 12 trang 104 Toán 9 Tập 1: Cho tam giác ABC có ba đỉnh nằm trên đường tròn (O) và AH là đường cao. Đường thẳng AO cắt đường tròn (O) tại điểm thứ hai D. Chứng minh rằng:

a) AC vuông góc với DC;

b) $\widehat{ABC}=\widehat{ADC};$

c) AB.AC = AH.AD.

Lời giải:

a) Xét đường tròn (O) có AD là đường kính, $\widehat{ACD}$ là góc nội tiếp chắn nửa đường tròn nên $\widehat{ACD}=90°,$ hay AC vuông góc với DC.

b) Xét đường tròn (O) có $\widehat{ABC},\widehat{ADC}$ là hai góc nội tiếp cùng chắn cung AC nên $\widehat{ABC}=\widehat{ADC}.$

c) Xét ∆ABH và ∆ADC có:

$\widehat{AHB}=\widehat{ACD}=90°;\widehat{ABC}=\widehat{ADC}$ (câu b)

Do đó ∆ABH ᔕ ∆ADC (g.g).

Suy ra $\frac{AB}{AD}=\frac{AH}{AC}$ (tỉ số các cạnh tương ứng) nên AB.AC = AH.AD.

Lời giải bài tập Toán 9 Bài tập cuối chương 5 hay khác:

• Giải Toán 9 trang 103

• Giải Toán 9 trang 105