Giải Toán 9 trang 68 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 9 trang 68 Tập 1 trong Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông Toán 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 68.

Giải Toán 9 trang 68 Tập 1 Chân trời sáng tạo

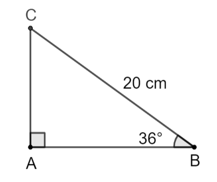
Thực hành 1 trang 68 Toán 9 Tập 1: Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 20 cm. Tính độ dài các cạnh góc vuông trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm):

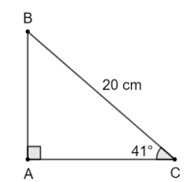
a) $\widehat{B}=36°;$

b) $\widehat{C}=41°.$

Lời giải:

a)

Xét tam giác ABC vuông tại A, $\widehat{B}=36°$ , ta có:

• AB = BC . cos B = 20 . cos 36° ≈ 16,18 (cm).

• AC = BC . sin B = 20 . sin 36° ≈ 11,76 (cm).

Vậy AB ≈ 16,18 cm; AC ≈ 11,76 cm.

b)

Xét tam giác ABC vuông tại A, $\widehat{C}=41°$ , ta có:

• AB = BC . sin C = 20 . sin 41° ≈ 13,12 (cm).

• AC = BC . cos C = 20 . cos 41° ≈ 15,09 (cm).

Vậy AB ≈ 13,12 cm; AC ≈ 15,09 cm.

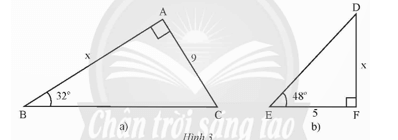
Thực hành 2 trang 68 Toán 9 Tập 1: Tính độ dài cạnh góc vuông x của mỗi tam giác vuông trong Hình 3 (kết quả làm tròn đến hàng phần trăm).

Lời giải:

a) Hình 3a: Xét tam giác ABC vuông tại A,$\widehat{B}=32°$ , ta có:

x = AB = AC . cot B = 9 . cot 32° ≈ 14,40.

Vậy x ≈ 14,40.

b) Hình 3b: Xét tam giác DEF vuông tại F, $\widehat{E}=48°$ , ta có:

x = DF = EF . tan E = 5 . tan 48° ≈ 5,55.

Vậy x ≈ 5,55.

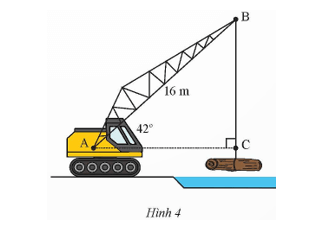
Vận dụng 1 trang 68 Toán 9 Tập 1: Một cần cẩu đang nâng một khối gõ trên sông. Biết tay cẩu AB có chiều dài là 16 m và nghiêng một góc 42° so với phương nằm ngang (Hình 4). Tính chiều dài BC của đoạn dây cáp (kết quả làm tròn đến hàng phần trăm).

Lời giải:

Xét tam giác ABC vuông tại C có $\widehat{A}=48°$ , ta có:

BC = AB . sin 42° = 16 . sin 42° ≈ 10,71 (m).

Vậy chiều dài BC của đoạn dây cáp khoảng 10,71 m.

Lời giải bài tập Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông hay khác:

• Giải Toán 9 trang 67
• Giải Toán 9 trang 71