Giải Toán 9 trang 77 Tập 1 Chân trời sáng tạo
Với Giải Toán 9 trang 77 Tập 1 trong Bài 1: Đường tròn Toán lớp 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 77.
Giải Toán 9 trang 77 Tập 1 Chân trời sáng tạo
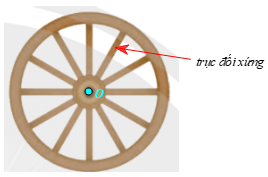
Thực hành 1 trang 77 Toán 9 Tập 1: Xác định tâm đối xứng và trục đối xứng của bánh xe trong Hình 7. Giải thích cách làm.
Lời giải:
⦁ Tâm đối xứng O của bánh xe là trục của bánh xe (hình vẽ);
⦁ Trục đối xứng của bánh xe là là các nan vành của bánh xe (hình vẽ).
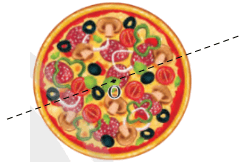
Vận dụng 1 trang 77 Toán 9 Tập 1: Nêu cách chia một cái bánh có dạng hình tròn tâm O (Hình 8) thành hai phần bằng nhau.
Lời giải:
Vì mọi đường thẳng đi qua tâm của đường tròn đều là trục đối xứng của nó, nên ta sẽ chia bánh thành hai phần bằng nhau bằng cách cắt qua tâm O của chiếc bánh (hình vẽ).
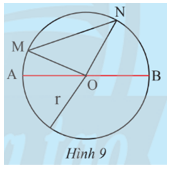
Khám phá 3 trang 77 Toán 9 Tập 1: Trên đường tròn (O; R), lấy bốn điểm A, B, M, N sao cho AB đi qua O và MN không đi qua O (Hình 9).
a) Tính độ dài đoạn thẳng AB theo R.
b) So sánh độ dài của MN và OM + ON. Từ đó, so sánh độ dài của MN và AB.
Lời giải:
a) Vì hai điểm A, B cùng nằm trên đường tròn (O; R) nên OA = OB = R.
Mà AB đi qua O hay O nằm giữa A, B nên AB = OA + OB = R + R = 2R.
Vậy AB = 2R.
b) Xét ∆OMN có: OM + ON > MN (bất đẳng thức trong tam giác). (1)
Ta có hai điểm M, N cùng nằm trên đường tròn (O; R) nên OM = ON = R.
Do đó từ (1) ta có R + R > MN hay 2R > MN.
Mà AB = 2R (câu a) nên AB > MN.
Lời giải bài tập Toán 9 Bài 1: Đường tròn hay khác: