Giải Toán 9 trang 82 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 9 trang 82 Tập 1 trong Bài 1: Đường tròn Toán lớp 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 82.

Giải Toán 9 trang 82 Tập 1 Chân trời sáng tạo

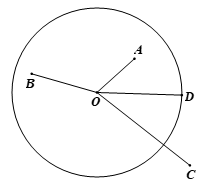
Bài 1 trang 82 Toán 9 Tập 1: Cho đường tròn (O), bán kính 5 cm và bốn điểm A, B, C, D thoả mãn OA = 3 cm, OB = 4 cm, OC = 7 cm, OD = 5 cm. Hãy cho biết mỗi điểm A, B, C, D nằm trong, nằm trên hay nằm ngoài đường tròn (O).

Lời giải:

Với R = 5 cm, ta có:

⦁ 3 < 5 hay OA < R nên điểm A nằm trong đường tròn;

⦁ 4 < 5 hay OB < R nên điểm B nằm trong đường tròn;

⦁ 7 > 5 hay OC > R nên điểm C nằm ngoài đường tròn;

⦁ 5 = 5 hay OD = R nên điểm D nằm trên đường tròn.

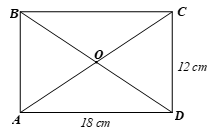
Bài 2 trang 82 Toán 9 Tập 1: Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Lời giải:

⦁ Vì ABCD là hình chữ nhật nên AC = BD. (1)

Gọi O là giao điểm của hai đường chéo AC, BD của hình chữ nhật.

Khi đó, O là trung điểm của AC và BD (tính chất hình chữ nhật) nên $OA=OC=\frac{1}{2}AC;$ $OB=OD=\frac{1}{2}BD.$(2)

Từ (1) và (2) ta có $OA=OC=OB=OD=\frac{1}{2}AC=\frac{1}{2}BD.$

Vậy bốn điểm A, B, C, D cùng thuộc một đường tròn đường kính AC, BD.

⦁ Vì ABCD là hình chữ nhật nên $\widehat{ADC}=90°.$

Xét ∆ADC vuông tại D, theo định lí Pythagore, ta có:

AC² = AD² + DC² = 18² + 12² = 468.

Do đó $AC=\sqrt{468}=\sqrt{6^2\cdot 13}=6\sqrt{13}\text{ (cm).}$

Vậy bán kính đường tròn đi qua bốn điểm A, B, C, D là $\frac{1}{2}AC=\frac{1}{2}\cdot 6\sqrt{13}=3\sqrt{13}\text{ (cm).}$

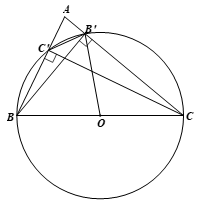
Bài 3 trang 82 Toán 9 Tập 1: Cho tam giác ABC có hai đường cao BB’ và CC’. Gọi O là trung điểm của BC.

a) Chứng minh đường tròn tâm O bán kính OB’ đi qua B, C, C’.

b) So sánh độ dài hai đoạn thẳng BC và B’C’.

Lời giải:

a) Xét ∆BCB’ vuông tại B’ có đường trung tuyến B’O ứng với cạnh huyền BC, do đó $B^{\text{'}}O=\frac{1}{2}BC.$

Mà O là trung điểm của BC nên $OB=OC=\frac{1}{2}BC.$

Do đó $B^{\text{'}}O=OB=OC=\frac{1}{2}BC.$

Chứng minh tương tự đối với ∆BCC’ vuông tại C’, ta cũng có $C^{\text{'}}O=OB=OC=\frac{1}{2}BC.$

Suy ra $B^{\text{'}}O=C^{\text{'}}O=OB=OC=\frac{1}{2}BC.$

Vậy đường tròn tâm O bán kính OB’ đi qua B, C, C’.

b) Xét đường tròn tâm O bán kính OB’, dây BC là đường kính đi qua tâm O, dây B’C’ là dây cung không đi qua tâm O.

Do đó BC > B’C’.

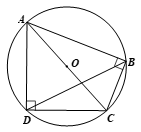
Bài 4 trang 82 Toán 9 Tập 1: Cho tứ giác ABCD có $\widehat{\text{B}}=\widehat{\text{D}}=90°.$

a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.

b) So sánh độ dài của AC và BD.

Lời giải:

a) Gọi O là trung điểm của AC. Khi đó $OA=OC=\frac{1}{2}AC.$

Xét ∆ABC vuông tại B có đường trung tuyến BO ứng với cạnh huyền AC, do đó $BO=\frac{1}{2}AC.$

Suy ra $OA=OB=OC=\frac{1}{2}AC.$(1)

Chứng minh tương tự đối với ∆ADC vuông tại D, ta cũng có: $OA=OD=OC=\frac{1}{2}AC.$(2)

Từ (1) và (2) suy ra $OA=OB=OC=OD=\frac{1}{2}AC.$

Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn đường kính AC.

b) Xét đường tròn tâm O đường kính AC có BD là dây cung không đi qua tâm O nên AC > BD.

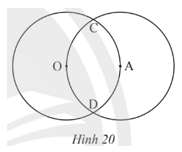
Bài 5 trang 82 Toán 9 Tập 1: Cho hai đường tròn (O; 2 cm) và (A; 2 cm) cắt nhau tại C, D, điểm A nằm trên đường tròn tâm O (Hình 20).

a) Vẽ đường tròn (C; 2 cm).

b) Đường tròn (C; 2 cm) có đi qua hai điểm O và A không? Vì sao?

Lời giải:

a) Mở một chiếc compa sao cho hai đầu compa cách nhau một khoảng bằng 2 cm. Đặt đầu nhọn của compa lên điểm C, xoay compa để đầu bút của compa vạch trên giấy một đường tròn, ta được đường tròn (C; 2 cm).

b) Vì C là giao điểm của hai đường tròn (O; 2 cm) và (A; 2 cm) nên C nằm trên cả hai đường tròn, do đó OC = 2 cm và CA = 2 cm.

Suy ra hai điểm O, A cùng nằm trên đường tròn (C; 2 cm).

Vậy đường tròn (C; 2 cm) đi qua hai điểm O và A.

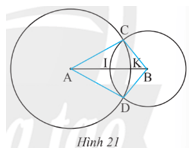
Bài 6 trang 82 Toán 9 Tập 1: Cho hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D, AB = 8 cm. Gọi K, I lần lượt là giao điểm của hai đường tròn đã cho với đoạn thẳng AB (Hình 21).

a) Tính độ dài của các đoạn thẳng CA, CB, DA và DB.

b) Điểm I có phải là trung điểm của đoạn thẳng AB không?

c) Tính độ dài của đoạn thẳng IK.

Lời giải:

a) Vì hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D nên C, D cùng nằm trên hai đường tròn (A; 6 cm) và (B; 4 cm), do đó AC = AD = 6 cm và BC = BD = 4 cm.

b) Do I là giao điểm của đường tròn (B; 4 cm) với đoạn thẳng AB nên I nằm giữa hai điểm A, B và I nằm trên đường tròn (B; 4 cm), do đó BI = 4 cm.

Vì I nằm giữa hai điểm A, B nên ta có: AI + IB = AB

Suy ra AI = AB – IB = 8 – 4 = 4 (cm).

Ta có I nằm giữa hai điểm A, B và AI = BI nên I là trung điểm của đoạn thẳng AB.

c) Do K là giao điểm của đường tròn (A; 6 cm) với đoạn thẳng AB nên K nằm trên đường tròn (A; 6 cm), do đó AK = 6 cm.

Ta có AI < AK (4 cm < 6 cm) nên I nằm giữa hai điểm A, K.

Do đó AI + IK = AK

Suy ra IK = AK – AI = 6 – 4 = 2 (cm).

Vậy IK = 2 cm.

Bài 7 trang 82 Toán 9 Tập 1: Xác định vị trí tương đối của (O; R) và (O’; R’) trong mỗi trường hợp sau:

a) OO’ = 18; R = 10; R’ = 6;

b) OO’ = 2; R = 9; R’ = 3;

c) OO’ = 13; R = 8; R’ = 5;

d) OO’ = 17; R = 15; R’ = 4.

Lời giải:

a) Ta có 18 > 10 + 6 nên OO’ > R + R’, suy ra hai đường tròn (O; R) và (O’; R’) ở ngoài nhau.

b) Ta có 2 < 9 – 3 nên OO’ < R – R’, suy ra đường tròn (O; R) đựng đường tròn (O’; R’).

c) Ta có 13 = 8 + 5 nên OO’ = R + R’, suy ra hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài.

d) Ta có 15 – 4 < 17 < 15 + 4 nên R – R’ < OO’ = R + R’, suy ra hai đường tròn (O; R) và (O’; R’) cắt nhau.

Lời giải bài tập Toán 9 Bài 1: Đường tròn hay khác:

• Giải Toán 9 trang 75
• Giải Toán 9 trang 77
• Giải Toán 9 trang 78
• Giải Toán 9 trang 81