Bài 5.6 trang 90 Toán 9 Kết nối tri thức Tập 1

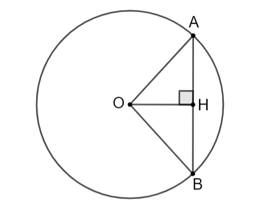
Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm.

Giải Toán 9 Bài 14: Cung và dây của một đường tròn - Kết nối tri thức

Bài 5.6 trang 90 Toán 9 Tập 1: Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm.

a) Tính khoảng cách từ O đến đường thẳng AB.

b) Tính tan α nếu góc ở tâm chắn cung AB bằng 2α.

Lời giải:

Bài 5.6 trang 90 Toán 9 Kết nối tri thức Tập 1

a) Gọi H là trung điểm của AB.

Suy ra $A H = \frac{A B}{2} = \frac{6}{2} = 3 (cm) .$

Xét ∆OAH và ∆OBH có:

OA = OB = R

Cạnh OH chung

HA = HB (do H là trung điểm của AB)

Do đó ∆OAH = ∆OBH (c.c.c).

Suy ra $\hat{O H A} = \hat{O H B}$ (hai góc tương ứng)

Mà $\hat{O H A}$ và $\hat{O H B}$ là hai góc bù nhau nên $\hat{O H A} + \hat{O H B} = 180 °$ hay $2 \hat{O H B} = 180 °$

Suy ra $\hat{O H A} = \hat{O H B} = 90 °$ nên OH ⊥ AB.

Do đó khoảng cách từ O đến đường thẳng AB bằng độ dài đoạn OH.

Xét tam giác OAH vuông tại H có:

AH² + OH²= OA² (định lý Pythagore)

Hay OH²= OA² − AH²= 5² − 3²= 16.

Nên OH = 4 cm.

Vậy khoảng cách từ O đến đường thẳng AB bằng 4 cm.

b) Theo giả thiết, góc ở tâm chắn cung AB là $\hat{A O B} = 2 α$ .

Từ câu a) ∆OAH = ∆OBH suy ra $\hat{H O A} = \hat{H O B}$ (hai góc tương ứng).

Lại có: $\hat{H O A} + \hat{H O B} = \hat{A O B}$ nên $2 \hat{H O A} = 2 α$ hay $\hat{H O A} = α .$

Suy ra $\tan α = \frac{A H}{O H} = \frac{3}{4} .$

Lời giải bài tập Toán 9 Bài 14: Cung và dây của một đường tròn hay, chi tiết khác: