Luyện tập 2 trang 83 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9
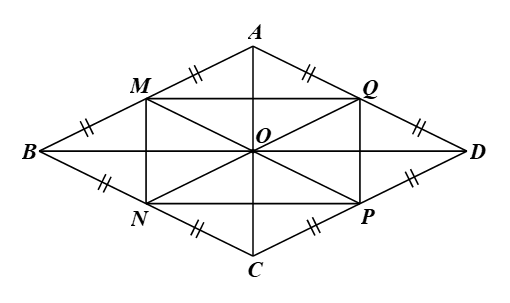
Cho hình thoi ABCD có các cạnh bằng 3 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng tỏ rằng tứ giác MNPQ là hình chữ nhật và tìm bán kính đường tròn ngoại tiếp của tứ giác đó.
Giải Toán 9 Bài 29: Tứ giác nội tiếp - Kết nối tri thức
Luyện tập 2 trang 83 Toán 9 Tập 2: Cho hình thoi ABCD có các cạnh bằng 3 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng tỏ rằng tứ giác MNPQ là hình chữ nhật và tìm bán kính đường tròn ngoại tiếp của tứ giác đó.
Lời giải:
⦁ Xét ∆ABC có M, N lần lượt là trung điểm của AB, BC nên MN là đường trung bình của tam giác. Do đó MN // AC và MN = AC. (1)
Chứng minh tương tự đối với ∆ACD, ta cũng có PQ // AC và PQ = AC. (2)
Từ (1) và (2) ta có MN // PQ và MN = PQ.
Do đó tứ giác MNPQ là hình bình hành.
Vì ABCD là hình thoi nên AC ⊥ BD. (3)
Xét ∆ABD có M, Q lần lượt là trung điểm của AB, AD nên MQ là đường trung bình của tam giác. Do đó MQ // BD. (4)
Từ (1), (3) và (4) suy ra MN ⊥ MQ hay
Khi đó hình bình hành MNPQ là hình chữ nhật.
⦁ Vì MNPQ là hình chữ nhật nên đường tròn ngoại tiếp hình chữ nhật có tâm là giao điểm hai đường chéo MP và NQ.
Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và BD.
Vì ABCD là hình thoi nên AB // CD và AB = CD.
Lại có M, P lần lượt là trung điểm của AB, CD nên AM = MB = CP = PD và AM // CP.
Do đó tứ giác AMCP là hình bình hành.
Suy ra hai đường chéo AC và MP cắt nhau tại trung điểm của mỗi đường.
Lại có O là trung điểm của AC nên O cũng là trung điểm của MP.
Khi đó, đường tròn ngoại tiếp hình chữ nhật MNPQ có tâm là điểm O và bán kính là OM.
Xét ∆ABC có M, O lần lượt là trung điểm của AB, AC nên MO là đường trung bình của tam giác. Do đó
Vậy bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng 1,5 cm.
Lời giải bài tập Toán 9 Bài 29: Tứ giác nội tiếp hay, chi tiết khác:
HĐ1 trang 80 Toán 9 Tập 2: Cho tứ giác ABCD có (H.9.28). Hãy giải thích ....
HĐ3 trang 81 Toán 9 Tập 2: Em hãy đo các góc đối nhau A và C của tứ giác ABCD trong HĐ2 ....
Luyện tập 1 trang 81 Toán 9 Tập 2: Cho tam giác ABC có các đường cao BE, CF. ....
HĐ4 trang 82 Toán 9 Tập 2: Vẽ hình chữ nhật ABCD và giao điểm M của hai đường chéo AC và BD ....
HĐ5 trang 82 Toán 9 Tập 2: Cho hình vuông ABCD có cạnh bằng 3 cm (H.9.34) ....
Thử thách nhỏ 2 trang 83 Toán 9 Tập 2: Nếu các hình chữ nhật có chung một đường chéo ....
Bài 9.18 trang 83 Toán 9 Tập 2: Cho ABCD là tứ giác nội tiếp. Tính số đo của các góc còn lại ....
Bài 9.19 trang 83 Toán 9 Tập 2: Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng ....
Bài 9.20 trang 83 Toán 9 Tập 2: Cho hình bình hành ABCD nội tiếp đường tròn (O) ....