Chứng minh ba điểm thẳng hàng (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Chứng minh ba điểm thẳng hàng lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Chứng minh ba điểm thẳng hàng.

Chứng minh ba điểm thẳng hàng (bài tập + lời giải)

1. Phương pháp giải.

- Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương. Hay A, B, C phân biệt thẳng hàng khi và chỉ khi tồn tại số thực k khác 0 sao cho: $\overrightarrow{AB}=k\overrightarrow{AC}$

- Sử dụng các tính chất, quy tắc về phép toán vectơ,... để biến đổi đưa về điều cần chứng minh.

2. Ví dụ minh họa.

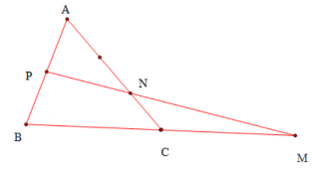
Ví dụ 1. Cho tam giác ABC có P là trung điểm của AB và M thuộc tia BC sao cho BC = CM, N thuộc cạnh AC sao cho AN = 2NC. Chứng minh rằng 3 điểm M, N, P thẳng hàng.

Hướng dẫn giải:

Vì M thuộc tia BC sao cho BC = CM nên $\overrightarrow{MC}=\overrightarrow{CB}$; vì N thuộc cạnh AC sao cho AN = 2NC nên $\overrightarrow{CN}=\frac{1}{3}\overrightarrow{CA}$.

Vì P là trung điểm AB nên $\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BA}$.

Ta có: $\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CA}$  (quy tắc ba điểm)

$\Rightarrow 3\overrightarrow{MN}=3\overrightarrow{CB}+\overrightarrow{CA}$ (1)

Lại có: $\overrightarrow{MP}=\overrightarrow{MB}+\overrightarrow{BP}=2\overrightarrow{CB}+\frac{1}{2}\overrightarrow{BA}$

$=2\overrightarrow{CB}+\frac{1}{2}\left(\overrightarrow{CA}-\overrightarrow{CB}\right)=2\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CA}-\frac{1}{2}\overrightarrow{CB}$

$=\frac{3}{2}\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CA}$

$\Rightarrow 2\overrightarrow{MP}=3\overrightarrow{CB}+\overrightarrow{CA}$ (2)

Từ (1) và (2) ta có: $3\overrightarrow{MN}=2\overrightarrow{MP}\iff \overrightarrow{MN}=\frac{2}{3}\overrightarrow{MP}$

Vậy 3 điểm M, N, P thẳng hàng.

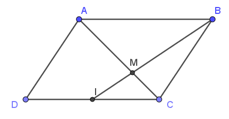
Ví dụ 2. Cho hình bình hành ABCD. Gọi I là trung điểm của CD. Lấy điểm M trên đoạn BI sao cho BM = 2MI. Chứng minh A, M, C thẳng hàng.

Hướng dẫn giải:

Ta có: $\overrightarrow{BM}=2\overrightarrow{MI}$

$\Rightarrow \overrightarrow{BA}+\overrightarrow{AM}=2\overrightarrow{MI}$ (*)

Vì ABCD là hình bình hành nên $\overrightarrow{BA}=\overrightarrow{CD}$

Mà I là trung điểm CD nên $\overrightarrow{CD}=2\overrightarrow{CI}$

Thay vào đẳng thức (*) ở trên ta có:

$2\overrightarrow{CI}+\overrightarrow{AM}=2\overrightarrow{MI}\iff \overrightarrow{AM}=2\overrightarrow{MI}+2\overrightarrow{IC}\iff \overrightarrow{AM}=2\overrightarrow{MC}$

Vậy A, M, C thẳng hàng.

3. Bài tập tự luyện.

Bài 1. Cho tam giác ABC có trọng tâm G, lấy các điểm I, J thỏa mãn: $\overrightarrow{IA}=2\overrightarrow{IB}, 3\overrightarrow{JA}+2\overrightarrow{JC}=\overrightarrow{0}$. Ba điểm nào sau đây thẳng hàng ?

A. A, B, G;

B. A, C, G;

C. A, I, G;

D. I, J, G.

Bài 2. Cho tam giác ABC, lấy các điểm M, N, P thỏa mãn:$\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}, 3\overrightarrow{AN}-2\overrightarrow{AC}=\overrightarrow{0}, \overrightarrow{PB}=2\overrightarrow{PC}$. Ba điểm nào sau đây thẳng hàng ?

A. M, N, P;

B. A, M, B;

C. A, N, C;

D. M, N, B.

Bài 3. Cho điểm A, B, C sao cho: $\overrightarrow{CA}-2\overrightarrow{CB}=\overrightarrow{0}$. Cho điểm M bất kỳ trong mặt phẳng và gọi $\overrightarrow{MN}$ là vectơ định bởi $\overrightarrow{MN}=\overrightarrow{MA}-2\overrightarrow{MB}$. Ba điểm nào sau đây thẳng hàng ?

A. M, N, A;

B. M, B, A;

C. M, N, C;

D. A, N, B.

Bài 4. Cho hình bình hành ABCD. Trên đoạn BC lấy điểm H, trên đoạn BD lấy điểm K sao cho: BH = CH, DK = 2BK. Ba điểm nào sau đây thẳng hàng ?

A. A, K, H;

B. A, B, C;

C. A, K, C;

D. B, K, H.

Bài 5. Cho hình bình hành ABCD. Trên BC lấy điểm H, trên BD lấy điểm K sao cho: $\overrightarrow{BH}=\frac{1}{5}\overrightarrow{BC}, \overrightarrow{BK}=\frac{1}{6}\overrightarrow{BD}$. Ba điểm nào sau đây thẳng hàng ?

A. A, K, H;

B. A, B, C;

C. A, K, C;

D. B, K, H.

 Bài 6. Cho tam giác ABC có M, N, P thỏa mãn: $\overrightarrow{MB}=3\overrightarrow{MC}, \overrightarrow{NA}+3\overrightarrow{NC}=\overrightarrow{0}, \overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}$. Ba điểm nào sau đây thẳng hàng ?

A. A, B, C;

B. M, N, A;

C. M, N, P;

D. B, N, C.

Bài 7. Cho tam giác ABC có trọng tâm G và điểm I sao cho: $\overrightarrow{IC}-\overrightarrow{IB}+\overrightarrow{IA}=\overrightarrow{0}$. Ba điểm nào sau đây thẳng hàng ?

A. I, G, C;

B. I, G, A;

C. I, A, B;

D. I, G, B.

Bài 8. Cho tam giác ABC có điểm I nằm trên cạnh AC sao cho $\overrightarrow{BI}=\frac{3}{4}\overrightarrow{AC}-\overrightarrow{AB}$, J là điểm thỏa mãn $\overrightarrow{BJ}=\frac{1}{2}\overrightarrow{AC}-\frac{2}{3}\overrightarrow{AB}$. Ba điểm nào sau đây thẳng hàng ?

A. I, J, C;

B. I, J, B;

C. I, A, B;

D. I, G, B.

Bài 9. Cho tam giác ABC có điểm D sao cho: $\overrightarrow{BD}=\frac{2}{3}\overrightarrow{BC}$ và I là trung điểm của AD. Gọi M là điểm thỏa mãn $\overrightarrow{AM}=x\overrightarrow{AC}$ với x là số thực. Để B, I, M thẳng hàng thì x = ?

A. 1;

B. 2;

C. $\frac{5}{2}$;

D. $\frac{2}{5}$.

Bài 10. Cho hình bình hành ABCD, I là trung điểm của cạnh BC và E là điểm thuộc đường chéo AC sao cho 3AE = 2AC. Ba điểm nào sau đây thẳng hàng ?

A. D, E, I;

B. D, E, C;

D. D, E, A;

C. A, I, E.