Giải bất phương trình bậc hai (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Giải bất phương trình bậc hai lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Giải bất phương trình bậc hai.

Giải bất phương trình bậc hai (bài tập + lời giải)

1. Phương pháp giải

a) Định nghĩa:

– Bất phương trình bậc hai ẩn x là bất phương trình có dạng:

ax² + bx + c > 0, ax² + bx + c ≥ 0, ax² + bx + c < 0, ax² + bx + c ≤ 0,

trong đó a, b, c là những số thực đã cho và a ≠ 0.

– Số thực x₀ gọi là một nghiệm của bất phương trình bậc hai ax² + bx + c > 0, nếu ax₀²  + bx₀ + c > 0.

Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai ax² + bx + c > 0 gọi là tập nghiệm của bất phương trình này.

– Giải bất phương trình bậc hai f(x) = ax² + bx + c > 0 là tìm tập nghiệm của nó.

b) Phương pháp giải bất phương trình bậc hai:

Bước 1. Xét dấu tam thức f(x) = ax² + bx + c.

Bước 2. Tìm các khoảng mà tam thức f(x) = ax² + bx + c có dấu phù hợp với yêu cầu và kết luận.

2. Ví dụ minh họa

Ví dụ 1. Giải các bất phương trình sau:

a) –3x² + 2x + 1 < 0.

b) x² + x – 12 ≤ 0.

Hướng dẫn giải:

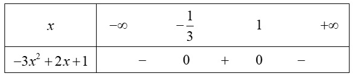
a) Xét f(x) = –3x² + 2x + 1

f(x) = –3x² + 2x + 1 = 0 ⇔ x = 1 hoặc $x=-\frac{1}{3}.$

Bảng xét dấu:

Từ bảng xét dấu, ta có tập nghiệm của bất phương trình f(x) < 0 là

$S=\left(-\infty ;-\frac{1}{3}\right)\cup \left(1;+\infty \right).$

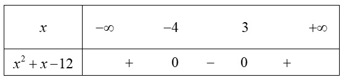
b) Xét f(x) = x² + x – 12

f(x) = x² + x – 12 = 0 ⇔ x = 3 hoặc x = –4.

Bảng xét dấu:

Từ bảng xét dấu, ta có tập nghiệm của bất phương trình f(x) ≤ 0 là S = [–4; 3].

Ví dụ 2. Giải các bất phương trình sau:

a) (1 – 2x)(x² – x – 1) > 0.

b) $\frac{x^2-1}{\left(x^2-3\right)\left(-3x^2+2x+8\right)}>0.$

c) $x^2+10\le \frac{2x^2+1}{x^2-8}.$

Hướng dẫn giải:

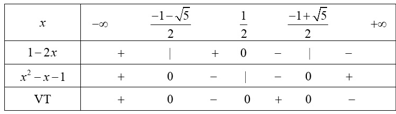
a) Ta có: (1 – 2x)(x² – x – 1) = 0

$\iff \left[\begin{array}{l}1–2x=0\\ x^2–x–1=0\end{array}\right.\iff \left[\begin{array}{l}x=\frac{1}{2}\\ x=\frac{1\pm \sqrt{5}}{2}\end{array}\right.$

Bảng xét dấu:

Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình là

$S=\left(–\infty ;\frac{1–\sqrt{5}}{2}\right)\cap \left(\frac{1}{2};\frac{1+\sqrt{5}}{2}\right).$

b) $\frac{x^2-1}{\left(x^2-3\right)\left(-3x^2+2x+8\right)}>0$

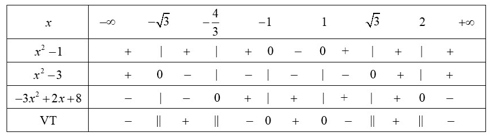
Ta có:

x² – 1 = 0 ⇔ x = ±1

x² – 3 = 0 ⇔ x = ±$\sqrt{3}$

–3x² + 2x + 8 = 0 ⇔ x = 2 hoặc $x=-\frac{4}{3}.$

Bảng xét dấu:

Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là $S=\left(-\sqrt{3};-\frac{4}{3}\right)\cup \left(-1;1\right)\cup \left(\sqrt{3};2\right).$

c) Bất phương trình $x^2+10\le \frac{2x^2+1}{x^2-8}$ tương đương với

$\frac{2x^2+1}{x^2-8}-\left(x^2+10\right)\ge 0$

$\iff \frac{2x^2+1-\left(x^2-8\right)\left(x^2+10\right)}{x^2-8}\ge 0$

$\iff \frac{81-x^4}{x^2-8}\ge 0$

$\iff \frac{\left(9-x^2\right)\left(9+x^2\right)}{\left(x^2-8\right)}\ge 0$

$\iff \frac{9-x^2}{x^2-8}\ge 0$ (vì x² + 9 ≥ 0 với mọi x)

Ta có  9 – x² = 0 ⇔ x = ±3

           x² – 8 = 0 ⇔ x = ±$2\sqrt{2}$

Bảng xét dấu:

Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình là $S=\left[-3;-2\sqrt{2}\right)\cup \left(2\sqrt{2};3\right].$

3. Bài tập tự luyện 

Bài 1. Tập nghiệm của bất phương trình: 2x² – 7x – 15 ≥ 0 là

A. $\left(–\infty ;–\frac{3}{2}\right]\cup \left[5;+\infty \right);$

B. $\left[–\frac{3}{2};5\right]$

C. $\left(–\infty ;–5\right]\cup \left[\frac{3}{2};+\infty \right)$

D. $\left[–5;\frac{3}{2}\right]$

Bài 2. Tập nghiệm của bất phương trình –x² + 6x + 7 ≥ 0 là

A. (–∞; –1] ∪ [7; +∞);

B. [–1; 7];

C. (–∞; –7] ∪ [1; +∞);

D. [–7; 1].

Bài 3. Tập nghiệm của bất phương trình –2x² + 3x – 7 ≥ 0 là

A. S = 0;

B. S = {0};

C. S = Ø;

D. S = ℝ.

Bài 4. Tập nghiệm của bất phương trình x² – 3x + 2 < 0 là

A. (–∞; 1) ∪ (2; +∞);

B. (2; +∞);

C. (1; 2);

D. (–∞; 1).

Bài 5. Số thực x dương lớn nhất thỏa mãn x² – x – 12 ≤ 0 là

A. 1;

B. 2;

C. 3;

D. 4.

Bài 6. Bất phương trình nào sau đây có tập nghiệm là ℝ?

A. –3x² + x – 1 ≥ 0;

B. –3x² + x – 1 > 0;

C. –3x² + x – 1 < 0;

D. –3x² + x – 1 ≤ 0.

Bài 7. Cho bất phương trình x² – 8x + 7 ≥ 0. Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình?

A. (–∞; 0];

B. [8; +∞);

C. (–∞; 1);

D. [6; +∞).

Bài 8. Tập nghiệm của bất phương trình x(x + 5) ≤ 2(x² + 2) là

A. (–∞; 1];

B. [1; 4];

C. (–∞; 1] ∪ [4; +∞);

D. [4; +∞).

Bài 9. Tập nghiệm S của bất phương trình $\frac{x–7}{4x^2–19x+12}>0$ là

A. $S=\left(–\infty ;\frac{3}{4}\right)\cup \left(4;7\right);$

B. $S=\left(\frac{3}{4};4\right)\cup \left(7;+\infty \right);$

C. $S=\left(\frac{3}{4};4\right)\cup \left(4;+\infty \right);$

D. $S=\left(\frac{3}{4};7\right)\cup \left(7;+\infty \right).$

Bài 10. Có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình $\frac{x^4–x^2}{x^2+5x+6}\le 0?$

A. 0;

B. 2;

C. 1;

D. 3.