Giải toán bằng biểu đồ Ven (bài tập + lời giải)
Haylamdo sưu tầm bài viết phương pháp giải bài tập Giải toán bằng biểu đồ Ven lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Giải toán bằng biểu đồ Ven.
Giải toán bằng biểu đồ Ven (bài tập + lời giải)
1. Phương pháp giải
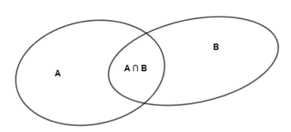
Trong toán học, người ta thường minh họa tập hợp bằng một hình phẳng được bao quanh bởi một đường cong khép kín, gọi là biểu đồ Ven.
+ Giải toán bằng biểu đồ Ven là sử dụng các đường cong khép kín giao nhau để mô tả các đại lượng và mối quan hệ giữa chúng.
+ Biểu đồ Ven cho ta cách nhìn trực quan và mối quan hệ giữa các đại lượng từ đó tìm ra yếu tố chưa biết.
Phương pháp giải toán sử dụng biểu đồ Ven:
+ Bước 1: Chuyển bài toán về ngôn ngữ tập hợp.
+ Bước 2: Sử dụng sơ đồ Ven để minh họa các tập hợp.
Vẽ các vòng kín đại diện các tập hợp (mỗi vòng kín là một tập hợp), lưu ý hai vòng kín có phần chung nếu mỗi vòng kín có ít nhất một phần nằm trong vòng kín kia và hai tập hợp đó khác rỗng.
+ Bước 3: Dựa vào sơ đồ Ven ta thiết lập được đẳng thức hoặc phương trình, hệ phương trình, từ đó tìm được kết quả bài toán.
Lưu ý:
+ Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
⇒ n(A ∩ B) = n(A) + n(B) – n(A ∪ B).
+ Nếu A và B không có phần tử chung, tức là A ∩ B = ∅, thì n(A ∪ B) = n(A) + n(B).
2. Ví dụ minh họa
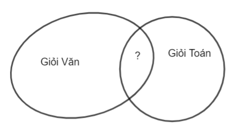
Ví dụ 1: Lớp 10A có 30 học sinh giỏi, trong đó có 20 học sinh giỏi Văn, 15 học sinh giỏi Toán. Hỏi có bao nhiêu học sinh vừa giỏi Văn vừa giỏi Toán?
Hướng dẫn giải:
Dựa vào đề bài, ta có biểu đồ Ven như sau:
Gọi A là tập hợp các học sinh giỏi Văn trong lớp 10A, B là tập hợp các học sinh giỏi Toán trong lớp 10A.
Theo bài ra ta có:
Số học sinh giỏi Văn là 20 hay n(A) = 20.
Số học sinh giỏi Toán là 15 hay n(B) = 15.
Tập hợp các bạn học sinh giỏi ít nhất một môn là A ∪ B.
Do đó, n(A ∪ B) = 30.
Tập hợp các bạn vừa giỏi Văn vừa giỏi Toán là A ∩ B.
Do đó số bạn học sinh vừa giỏi Văn vừa giỏi Toán được tính như sau:
n(A ∩ B) = n(A) + n(B) – n(A ∪ B) = 20 + 15 – 30 = 5.
Vậy lớp 10A có 5 bạn vừa giỏi Văn vừa giỏi Toán.
Ví dụ 2: Một công ty đa quốc gia có 28 người nói Tiếng Anh, 24 người nói Tiếng Trung Quốc. Biết trong đó có 10 người vừa nói Tiếng Anh vừa nói Tiếng Trung Quốc. Hỏi công ty trên có bao nhiêu người nói ít nhất một trong hai thứ tiếng trên?
Hướng dẫn giải:
Gọi A là tập hợp những người nói Tiếng Anh, B là tập hợp những người nói Tiếng Trung Quốc.
Theo đề ra ta có:
– Số người nói Tiếng Anh là n(A) = 28.
– Số người nói Tiếng Trung Quốc là n(B) = 24.
Những người vừa nói Tiếng Anh vừa nói Tiếng Trung Quốc là những người thuộc tập hợp A ∩ B.
Do đó, n(A ∩ B) = 10.
Những người nói được ít nhất một thứ tiếng là những phần tử thuộc tập hợp A ∪ B.
n(A ∪ B) = n(A) + n(B) – n(A ∩ B) = 28 + 24 – 10 = 42.
Vậy có 42 người nói ít nhất một trong hai thứ tiếng trên.
3. Bài tập tự luyện
Bài 1: Cho tập hợp A có 9 phần tử, tập hợp B có 5 phần tử, tập hợp A ∩ B có 3 phần tử. Tính số phần tử của tập hợp A \ B.
A. 5;
B. 6;
C. 7;
D. 8.
Bài 2: Cho tập hợp A có 15 phần tử, tập hợp B có 10 phần tử, tập hợp A ∩ B có 5 phần tử. Tính số phần tử của tập hợp B \ A.
A. 2;
B. 3;
C. 4;
D. 5.
Bài 3: Cho tập hợp A có 12 phần tử, tập hợp B có 15 phần tử, tập hợp A ∩ B có 6 phần tử. Tính số phần tử của tập hợp A ∪ B.
A. 20;
B. 21;
C. 22;
D. 23.
Bài 4: Cho tập hợp A có 19 phần tử, tập hợp B có 22 phần tử, tập hợp các phần tử hoặc thuộc A hoặc thuộc B gồm 35 phần tử. Tính số phần tử của tập hợp A vừa thuộc A vừa thuộc B.
A. 6;
B. 7;
C. 8;
D. 9.
Bài 5: Để tổ chức một buổi đi liên hoan, lớp 10B lập một bài khảo sát. Kết quả là có 20 bạn rảnh vào thứ 7, 25 bạn rảnh vào chủ nhật. Trong đó có 8 bạn rảnh cả hai ngày.
Hỏi có bao nhiêu học sinh chỉ rảnh vào ngày thứ 7?
A. 10;
B. 11;
C. 12;
D. 13.
Bài 6: Trong môn thể dục, lớp 10C có 21 bạn đăng kí học bơi, 30 bạn đăng kí học môn cầu lông, 10 bạn vừa đăng kí học bơi vừa đăng kí cầu lông. Hỏi lớp 10C có tất cả bao nhiêu bạn, biết mỗi bạn đều đang kí học bơi hoặc học cầu lông?
A. 40;
B. 41;
C. 42;
D. 43.
Bài 7: Lớp 10D có 22 học sinh thích chơi bóng đá, 17 học sinh thích chơi môn cờ vua, 7 học sinh thích cả hai môn bóng đá và cờ vua và 10 bạn không thích chơi môn nào cả. Hỏi lớp 10D có bao nhiêu học sinh?
A. 39;
B. 40;
C. 41;
D. 42.
Bài 8: Lớp 10T có 23 học sinh thích học môn Toán, 11 học sinh thích học môn Tiếng Anh, 5 học sinh thích học cả hai môn Toán và Tiếng Anh và 12 bạn không thích học môn nào cả (trong hai môn Toán và Tiếng Anh). Hỏi lớp 10T có bao nhiêu học sinh chỉ thích một môn?
A. 26;
B. 28;
C. 24;
D. 30.
Bài 9: Cho tập hợp A có 10 phần tử, tập hợp B có 12 phần tử, tập hợp các phần tử hoặc thuộc A hoặc thuộc B gồm 20 phần tử. Tính số phần tử của tập hợp A ∩ B.
A. 2;
B. 5;
C. 6;
D. 8.
Bài 10: Cho tập hợp A có 18 phần tử, tập hợp B có 25 phần tử, tập hợp A ∩ B có 9 phần tử. Tính số phần tử chỉ thuộc tập hợp A.
A. 8;
B. 9;
C. 10;
D. 11.